Procedure di Cluster
analysis con S-Plus.
Nuove tecniche
per la costruzione di gruppi.
Calcolo della matrice
di dissimilarità *
_Variabili continue *
__Distanza di Minkowski: *
__Distanza Manhattan: *
__Distanza Euclidea: *
_Variabili binarie *
_Variabili
nominali *
_Variabili
ordinali *
_Variabili
numeriche ratio-scaled *
_Variabili
miste *
_La funzione daisy *
Partizionamento
attorno ai medoidi (k-medoids) *
_La funzione pam *
_La funzione clara *
Cluster sfocata *
_La funzione fanny *
La Cluster Analysis è un insieme
di tecniche statistiche che hanno come obiettivo
la costruzione di gruppi di unità tali
per cui siano massime l'omogeneità all'interno
dei gruppi e la differenza tra i gruppi, in altri
termini che gli oggetti all'interno di un cluster
si assomiglino tra loro mentre oggetti in cluster
diversi siano dissimili.
In linea generale, per costruire dei gruppi di
unità, è necessario:
- definire i caratteri rispetto a cui effettuare
il raggruppamento delle unità,
- definire una misura del grado di diversità
tra le coppie di unità,
- scegliere un algoritmo con cui procedere alla
ricerca dei cluster.
La classificazione più diffusa dei metodi
di cluster è basata sull'algoritmo e ,li
distingue in:
- metodi gerarchici
- metodi non gerarchici.
In questo documento verranno trattate alcune
procedure di S-Plus specificatamente sviluppate
per la cluster analysis, in particolare verranno
affrontati i seguenti argomenti:
- costruzione della matrice
di dissimilarità utilizzando la procedura
daisy
di S-Plus
- l'algoritmo di tipo non
gerarchico di partizionamento attorno ai medoidi
(procedure pam
e clara)
- l'algoritmo di cluster
sfocata fanny.
Calcolo della matrice
di dissimilarità
Una volta scelte le variabili rispetto alle quali
procedere alla costruzione dei gruppi, il primo
passaggio è definire un criterio rispetto
a cui misurare quanto due unità sono simili
in riferimento a tutti i caratteri prescelti.
Tradizionalmente viene utilizzata la matrice
di distanza, costruita su variabili continue ed
utilizzando diverse misure della distanza (euclidea,
manhattan,…).
La procedura daisy costruisce una matrice detta
di dissimilarità, utilizzando sia variabili
continue sia variabili categoriche (binarie, ordinali
o nominali)-
Indichiamo con
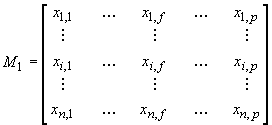 la matrice n oggetti x p variabili dei dati
la matrice n oggetti x p variabili dei dati
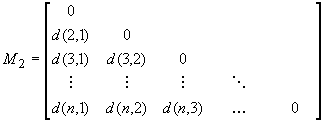 la matrice nxn di dissimilarità
la matrice nxn di dissimilarità
dove
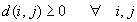 è la misura di dissimilarità tra
gli oggetti i e j.
è la misura di dissimilarità tra
gli oggetti i e j.
Variabili continue
Nel caso di queste variabili è necessaria
una standardizzazione dei dati per evitare la
dipendenza del valore dell’unità di misura
delle variabili. Per il calcolo della misura
standardizzata, detta z-score, è
conveniente fare uso della deviazione assoluta
media:
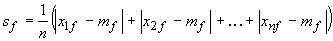 deviazione assoluta media
deviazione assoluta media
dove
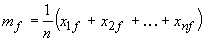
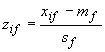 z-score
z-score
La deviazione assoluta media è più
robusta della deviazione standard, infatti 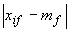 non è elevato al quadrato, riducendo i
problemi dovuti a outliers
non è elevato al quadrato, riducendo i
problemi dovuti a outliers
Per misurare la similarità tra due oggetti
i cui attributi sono variabili continue, viene
utilizzata normalmente una funzione-distanza.
Distanza di Minkowski:
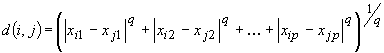
dove 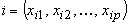 e
e 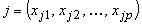 sono due oggetti p-dimensionali, e dove q è
un intero positivo.
sono due oggetti p-dimensionali, e dove q è
un intero positivo.
Questa distanza permette di incrementare o decrementare
il peso assegnato a dimensioni lungo le quali
gli oggetti risultano molto diversi:
Distanza Manhattan:
E' il caso in cui, nella distanza di Minkowski,
q=1
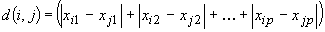
Distanza Euclidea:
E' il caso in cui, nella distanza di Minkowski,
q=2
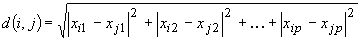
E' il tipo di distanza più utilizzata,
e rappresenta la distanza geometrica di un punto
in uno spazio multi-dimensionale. Sono valide
le seguenti proprietà:
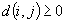
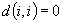
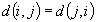
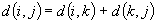
Variabili binarie
Sono variabili per cui sono possibili due stati:
"0" oppure "1". Si distinguono in
- simmetriche se i due stati sono equivalenti,
cioè se non vi sono preferenze su quale
stato debba essere codificato con "1";
- asimmetriche, se invece gli stati della
variabile non sono equivalenti
nel caso di variabili binarie, per determinare
la similarità di due oggetti si può
ricorrere ad una tabella di contingenza:

| |
|
|
oggetto
j |
|
| |
|
1 |
0 |
somma |
| |
1 |
a |
b |
a+b |
| oggetto
i |
0 |
c |
d |
c+d |
| |
somma |
a+c |
b+d |
p |
Il grado di similarità viene poi calcolato
mediante un coefficiente di corrispondenza:
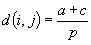 coefficiente
di Corrispondenza Semplice per variabili binarie
simmetriche coefficiente
di Corrispondenza Semplice per variabili binarie
simmetriche
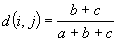 coefficiente di Jaccard per variabili binarie
asimmetriche
coefficiente di Jaccard per variabili binarie
asimmetriche
Variabili nominali
Sono variabili che possono assumere più
stati, ad esempio: "bianco", "rosso", "blu", e
possono essere considerate come una generalizzazione
delle variabili binarie da 2 ad n stati.
Per determinare la similarità tra due
oggetti si può calcolare un coefficiente
di corrispondenza semplice:
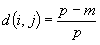
dove p = numero di variabili e m = numero di
corrispondenze; in alternativa si può creare
una nuova variabile binaria per ciascuno degli
m stati nominali.
Variabili ordinali
Una variabile ordinale è in pratica una
variabile nominale con un ordine tra i valori
assunti
Per misurare la similarità nel caso di
variabili ordinali, queste vengono trattate come
continue:
- si assegna un rango numerico ad ogni valore
assunto
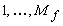
- si sostituiscono le
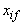 nominali
con i rispettivi ranghi nominali
con i rispettivi ranghi 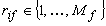 numerici
numerici
- si mappano i valori di ciascuna variabile
sull’intervallo [0, 1] rimpiazzando l’i-esimo
valore della f-esima variabile con
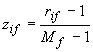
- si calcola la dissimilarità tra variabili
ordinali come se fossero variabili numerico
di tipo continuo
Variabili numeriche ratio-scaled
Si tratta di variabili numeriche misurate su
una scala non lineare di valori, ad esempio su
una scala esponenziale. Può quindi risultare
problematico misurare le distanze a causa della
distorsione della scala, potremo infatti avere
distanze piccole tra valori consecutivi vicini
allo zero e distanze grandi tra valori lontani
dallo zero.
Per ovviare a questo problema di scala si può:
- applicare una trasformazione (logaritmica)
in modo da trasformarli in variabili continue,
- considerare i valori come ordinali, assegnando
un rango e applicare la distanza usata per variabili
numeriche di tipo continuo.
Variabili miste
Nella pratica capita però che vengano
osservate, per ciascuna unità/oggetto,
una molteplicità di caratteri espressi
in variabili di tipi diversi. Per determinare
la misura di similarità tra due oggetti
caratterizzati da un set misto di variabili si
può utilizzare una formula che combini
i loro effetti.
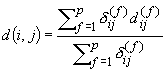 [1]
[1]
dove:
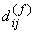 =
contributo della variabile =
contributo della variabile 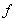 a
a 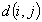 e che dipende dal tipo di variabile
e che dipende dal tipo di variabile
- se
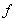 binaria o nominale:
binaria o nominale: 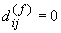 se se
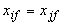 ,
e ,
e 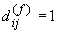 altrimenti
altrimenti
- se
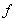 continua
continua 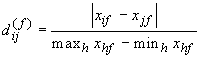 (distanza assoluta normalizzata)
(distanza assoluta normalizzata)
- se
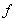 ordinale o ratio-scaled: vengono calcolati i
ranghi
ordinale o ratio-scaled: vengono calcolati i
ranghi 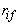 e
e 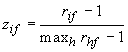
che vengono trattati come variabili continue.
e dove:
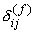 =
peso della variabile =
peso della variabile 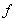 ,
con: ,
con:
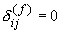 se
se 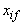 o
o 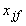 sono missing
sono missing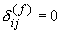 se
se 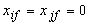 e la variabile
e la variabile 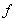 e binaria asimmetrica
e binaria asimmetrica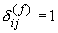
altrimenti
La
funzione daisy
La procedura daisy,
presente in S-Plus, calcola una matrice di dissimilarità
utilizzando la formula [1].
La sintassi è la seguente:
daisy(x, metric = "euclidean",
stand = F, type = list())
dove:
|
x |
è
la matrice dei dati; le colonne di tipo
numeric
verranno automatiche considerate variabili
continue, quelle di tipo factor
come variabili nominali, e quelle orederd
come variabili ordinali, gli altri tipi
dovranno essere specificati con l'opzione
type. |
|
metric |
consente di specificare la mterica per
il calcolo delle distanze per le variabili
continue; le opzioni possibili sono:
- euclidean,
che detrmina la distanza come radice della
somma dei quadrati delle differenze;
- manhattan
in cui le distanze sono calcolate come
somma delle differenze assolute.
Questa opzione è
utilizzata solo se tutte le variabili sono
di tipo numeric. |
|
stand |
con
questa opzione si indica se i dati della
matrice x
debbono essere o meno standardizzati prima
di procedere al calcolo della matrice di
dissimilarità, le modalità
sono:
- T
(true) per effettuare la standardizzazione,
- F
(false) per non effettuarla.
Anche in questo se non tutte le variabili
sono numeriche, l'opzione viene ignorata. |
|
type |
consente di definire i tipi di variabile
presenti nella matrice dei dati, se non
sono tra le tipologie di variabili che vengono
automaticamente riconosciute; la lista può
contenere i seguenti tipi:
- ordratio
se si tratta di variabili,
- ratio-scaled
che saranno trattate come ordinali,
- logratio
per le variabili ratio-scaled che richiedono
una trsformazione logaritmica,
- asym
per le variabili binarie asimmetriche
|
tess.diss <- daisy(tes.dat, type=list(asymm=c("NEWPROD",
"NEWPROC", "PRESPC", "EMAIL", "INTERNET")))
Partizionamento attorno
ai medoidi (k-medoids)
L'algoritmo comunemente utilizzato per la costruzione
di gruppi, nell'ambito dei non gerarchici, è
quello delle k-means. Lo ricordiamo brevemente:
fissato k, ovvero il numero di cluster che si
vogliono ottenere, i) vengono ripartiti
gli n oggetti casualmente nei k gruppi, ii)
vengono calcolati i punti medi dei cluster (centroidi),
iii) viene assegnato ciascun punto al cluster
il cui centro risulta essere il più vicino,
iv) si calcolano nuovamente i centroidi
(punti medi)dei gruppi, v) si ripete l'operazione
ripartendo dal secondo punto, e si termina quando
l'assegnamento dei punti non cambia più.
Il partizionamento attorno ai medoidi, detto
anche k-medoids, si basa invece sulla ricerca
di oggetti rappresentativi all'interno dei dati.
Questi punti, detti medoidi, sono determinati
in modo tale che la dissimilarità totale
di tutti i punti dai medoidi più vicini
sia minima. Si tratta quindi di trovare l'insieme
dei medoidi 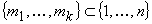 che minimizza la funzione obiettivo:
che minimizza la funzione obiettivo:
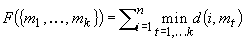 [2]
[2]
L'algoritmo è sostanzialmente diviso in
due fasi:
fase 1: BUILD in cui vengono individuati
i medoidi iniziali
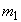 è l'oggetto per cui è minimo
è l'oggetto per cui è minimo 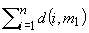 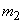 è l'oggetto che riduce il più
possibile la funzione obiettivo
è l'oggetto che riduce il più
possibile la funzione obiettivo 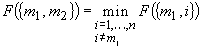 - …..
fase 2: SWAP, in cui si verifica se sono
possibili delle modifiche dei medoidi:
finché il processo non converge si considerano
tutte le coppie di oggetti 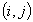 con
con 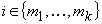 e
e 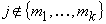 e si sostituisce
e si sostituisce 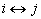 se ciò comporta una diminuzione della funzione
obiettivo.
se ciò comporta una diminuzione della funzione
obiettivo.
Confrontando gli algoritmi k-means e k-medoid
si può notare che:
- k-medoids può essere utilizzato anche
se il tipo di dati non consente di definire
la media (come ad esempio nel caso di dati categorici);
- l'obiettivo di k-means è la minimizzazione
della dei quadrati della distanza euclidea,
assumendo implicitamente che ogni cluster abbia
una distribuzione normale;
- k-medoids è più robusta perché
minimizza una somma di distanze assolute, rendendola
meno sensibile a possibili outlier;
- k-medoids non richiede alcuna congettura sui
centri iniziali, al contrario di k-means;
- entrambi richiedono la definizione iniziale
del numero di cluster
- questo algoritmo è
inefficiente e "funziona bene" solo su piccoli
data-set, in alternativa si può utilizzare
la procedura alternativa (denominata clara),
che utilizza un algoritmo di tipo k-medoids
su campioni casuali, ma questa randomizzazione
può condurre a risultati diversi.
La
funzione pam
La funzione pam,
implementata in S-Plus,
è una procedura di cluster analysis basata
sull'algoritmo dei k-medoids sopra descritto.
Oltre a costruire i gruppi fornisce anche un indice
della qualità del partizionamento degli
oggetti che consente di determinare quale sia
il numero ottimale di gruppi.
Per ogni unità i indichiamo
con A il cluster
a cui appartiene e calcoliamo
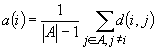 = dissimilarità media di i da tutti gli
altri oggetti di A.
= dissimilarità media di i da tutti gli
altri oggetti di A.
Consideriamo poi ogni cluster
C diverso da
A e calcoliamo:
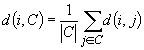 = dissimilarità media di i da tutti gli
oggetti di C.
= dissimilarità media di i da tutti gli
oggetti di C.
Dopo avere calcolato 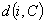 per tutti i cluster
per tutti i cluster 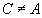 consideriamo la minore:
consideriamo la minore:
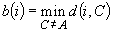
Il gruppo, che indichiamo
con B, per il
quale si registra il minimo è detto neighbor
dell'oggetto i, è il secondo miglior cluster
per l'unità i.
Calcoliamo quindi:
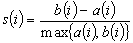 = silhouette width dell'unità i
= silhouette width dell'unità i
Il valore di 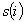 è sempre compreso tra -1 e 1, per cui può
essere interpretato come segue:
è sempre compreso tra -1 e 1, per cui può
essere interpretato come segue:
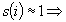 l'unità
i è ben classificata in A l'unità
i è ben classificata in A
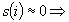 i
si trova tra due gruppi (tra A
e B) i
si trova tra due gruppi (tra A
e B)
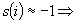 i
è mal classificato più vicino a
B che ad A. i
è mal classificato più vicino a
B che ad A.
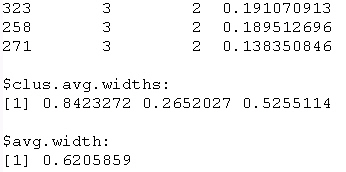
Sulla base dei silhoutte width è possibile
determinare la loro media complessiva che fornisce
un'indicazione sulla bontà globale della
cluster (detto anche silhouette coefficient SC),
oppure la media per singolo gruppo che invece
è indicativa della coesione del cluster.
I silhoutte width possono inoltre essere rappresentati
graficamente tramite un istogramma detto silhoutte
plot.
In S-Plus, la sintassi della
funzione pam
è la seguente:
pam(x, k, diss = F, metric = "euclidean",
stand = F)
dove:
|
x |
matrice dei dati o di dissimilarità |
|
k |
intero che indica il numero di gruppi da
costruire, deve essere 0 < k < n,
dove n è il numero di osservazioni |
|
diss |
può assumere valori F (false) se
la matrice x è una matrice di dati,
T (true) se invece è una matrice
di dissimilarità |
|
metric |
le opzioni possibili sono euclidean e manhattan
e rappresenta il tipo di metrica da utilizzare
per il calcolo delle dissimilarità,
se x è già una matrice di
dissimilarità il comando viene ignorato; |
|
stand |
può essere T (true) se si desidera
standardizzare i dati di x prima di procedere
al calcolo delle dissimilarità, anche
in questo caso se x è già
una matrice di dissimilarità il comando
viene ignorato |
tess.pam <- pam(tess.diss,3,diss=T)
Nell'esempio viene creato
un oggetto (tess.pam)
contenente tutte le informazioni sui gruppi. Gli
argomenti disponibili, riguardo a questo oggetto,
sono:
|
medoids |
elenca i centri (medoidi) dei gruppi |
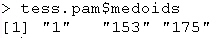
|
clustering |
fornisce il vettore dei gruppi di appartenenza
di ciascuna unità |

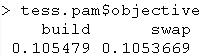
|
objective |
fornisce i valori della funzione obiettivo
al termine della prima (BUILD) e della seconda
(SWAP) fase della procedura di partizionamento
|
|
isolation |
visualizza un vettore di lunghezza pari
al numero di cluster, nel quale è
indicato se i gruppi sono isolati o meno.
Vengono identificati due tipologie di cluster
isolati: |
| |
L* = |
se
il suo diametro è più piccolo
del suo coefficiente di separazione, se
consideriamo il gruppo C,
sarà di tipo L* se 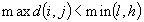 con
con 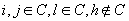 |
| |
L = |
se per ogni osservazione i la dissimilarità
massima tra i e ogni altro punto del gruppo
è inferiore alla dissimilarità
minima tra i e ogni altro punto di un altro
cluster; 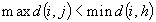 con
con 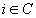 e
e 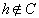 |
| |
Evidentemente un gruppo di tipo L* è
anche di tipo L. |
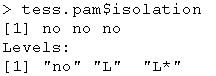
|
clusinfo |
visualizza una matrice con le caratteristiche
dei gruppi: |
| |
size: |
numerosità del cluster |
| |
max_diss: |
massima
distanza dal medoide del gruppo, se j
è il medoide del cluster C,
max_diss=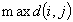 con
con 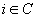 |
| |
av_diss:
|
distanza
media dal medoide del gruppo, se j
è il medoide del cluster C,
av_diss=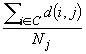
dove 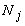 è la numerosità del cluster
escluso j
è la numerosità del cluster
escluso j |
| |
diameter: |
diametro del cluster, definita come distanza
massima tra oggetti del cluster,
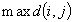 con
con 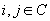
|
| |
separation: |
definita come la più piccola dissimilarità
tra due oggetti, uno appartenente al gruppo
e l'altro non appartenente,
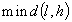 con
con 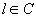 e
e 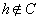
|

|
silinfo |
visualizza le informazioni sui silhoutte
width relativamente a ciascuna unità,
la media per gruppo e la media complessiva
(il silhouette coefficient) |

……
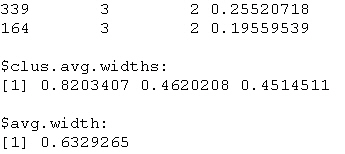
La procedura pam
fornisce inoltre un output grafico per mezzo del
comando plot:
plot(tess.pam)
I grafici prodotti sono 2, il primo è
un silhouette plot
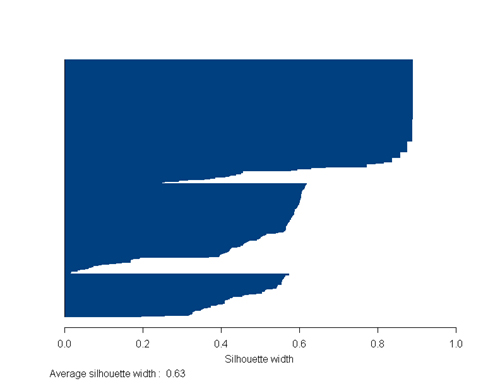
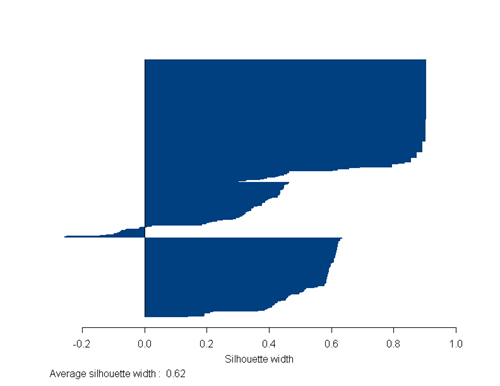
Il silhouette plot è utile per
decidere il numero ottimale di cluster, infatti
si può eseguire la procedura più
volte con valori diversi di k e confrontare i
risultati del silhouette plot, ed in particolare
la silhouette width media (SC).
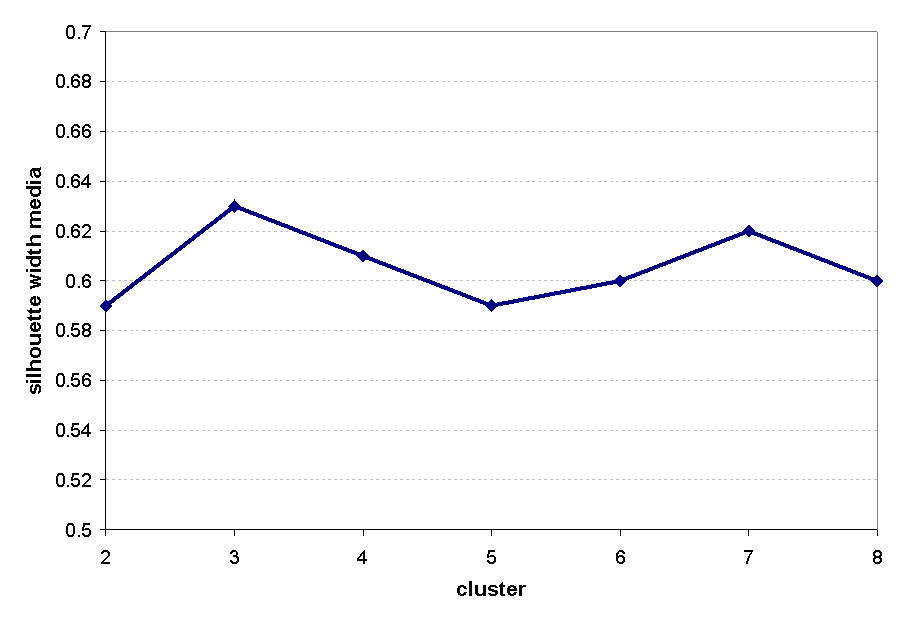
I valori di SC possono essere utilizzati per
valutare il grado di "intensità" della
struttura di raggruppamento, in particolare avremo
che:
intervallo di SC
0.71 - 1.00 è stata trovata una struttura
forte
0.51 - 0.70 è stata individuata una
struttura plausibile
0.26 - 0.50 la struttura è debole
< 0.26 non è stata individuata alcun
struttura
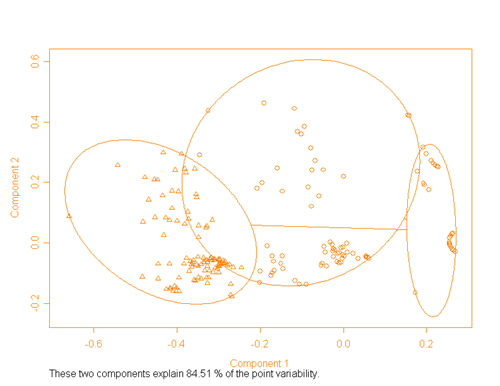
Il secondo grafico è il clusplot
che riporta su di un piano cartesiano i punti
dei cluster.
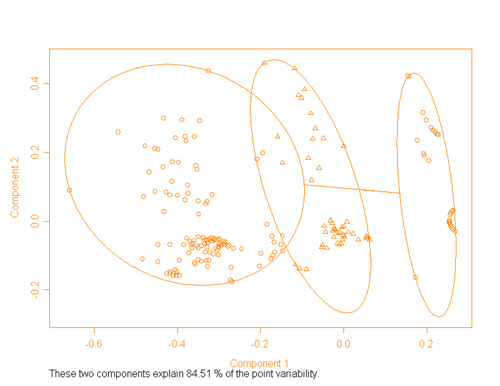
In particolare viene utilizzata una procedura
di multidimensional scaling (MDS) sulla matrice
di dissimilarità, vengono quindi utilizzate
le prime due componenti per visualizzare rispetto
ad esse i punti. Nel grafico di esempio le prime
due componenti spiegano oltre l'84% della variabilià.
I gruppi vengono inoltre evidenziati da un ellisse
e da marcatori diversi. Anche questo grafico può
essere utile per valutare la validità della
cluster elaborata, infatti in presenza di valori
alti della variabilità spiegata da parte
delle prime due componenti, è possibile
capire se siamo in presenza di una struttura di
raggruppamento più o meno forte.
La
funzione clara
La procedura pam
richiede elevate risorse di memoria per la sua
elaborazione; nel caso di grandi archivi di dati
può quindi divenire particolarmente oneroso
il ricorso a tale procedura, a questo scopo è
stata sviluppata la procedura clara
che sostanzialmente applica pam
su un set di campioni estratti dall'archivio.
La sintassi è la seguente:
clara(x,
k, metric = "euclidean", stand = F;
samples =
5, sampsize = 40 + 2 * k)
dove:
|
x |
matrice dei dati |
|
k |
numero di cluster da ottenere |
|
metric |
è il tipo di metrica da utilizzare
per il calcolo della matrice di dissimilarità,
può assumene valori "euclidean" o
"manhattan" |
|
stand |
T (true) se si vuole standardizzare i dati
prima di procedere al calcolo della matrice
di dissimilarità, in alternativa
F (false) |
|
samples |
numero di campioni da estrarre |
|
samplesize |
dimensione dei campioni da estrarre, se
non specificato viene assunto 40+2*k |
Operativamente vengono estratti tanti campioni
quanti indicati nell'opzione samples e per ognuno
di essi viene effettuato un clustering utilizzando
la procedura pam; vengono così determinati
i medoidi per ciascun campione, costruiti i gruppi
e calcolata la distanza media di ciascun punto
dal suo medoide; al termine della fase di estrazione
dei campioni viene considerato quello che ha fatto
registrare la minima distanza media. Alla fine
vengono quindi assegnati tutti i punti ai gruppi
utilizzando i centri individuati e viene calcolata
la distanza media dai medoidi utilizzando tutti
i punti.
Il vantaggio della procedura
clara
risiede nel fatto che può gestire data-set
più grandi rispetto a pam,
ma di contro è da precisare che la sua
efficienza dipende dalla dimensione dei campioni
estratti e che una "buona" cluster basata su un
campione non necessariamente costituisce una "buona"
cluster del collettivo da cui è estratto.
Cluster sfocata
Le procedure di cluster viste
in precedenza conducono all'assegnazione di un
punto ad un unico gruppo. Quindi se un oggetto
si trova tra due gruppi viene assegnato ad uno
solo di essi. Con una cluster sfocata ogni punto
viene invece associato un coefficiente di appartenenza
a ciascun gruppo. Se indichiamo con 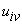 il coefficiente di appartenenza di ciascun punto
i a ciascun gruppo v,
tale coefficiente dovrà essere tale per
cui:
il coefficiente di appartenenza di ciascun punto
i a ciascun gruppo v,
tale coefficiente dovrà essere tale per
cui:
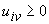 per ogni
per ogni 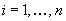 e per ogni
e per ogni 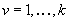 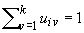 per ogni
per ogni 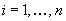
Il coefficiente viene determinato minimizzando
la funzione obiettivo:
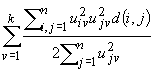
Per determinare quanto si sfocata l'appartenenza
di un punto ad un cluster viene calcolato il coefficiente
di partizione di Dunn:
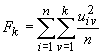
compreso 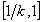 ,
di cui esiste una versione normalizzata compresa ,
di cui esiste una versione normalizzata compresa
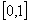 : :
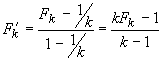
La
funzione fanny
In S-Plus è implementata
la funzione di fuzzy clustering denominata fanny.
La sintassi è la seguente:
fanny(x, k, diss = F, metric =
"euclidean", stand = F)
dove:
|
x |
matrice dei dati |
|
k |
numero di cluster da ottenere |
|
diss |
assume valore T (true) se x è una
matrice di dissimilarità |
|
metric |
è il tipo di metrica da utilizzare
per il calcolo della matrice di dissimilarità,
può assumene valori "euclidean" o
"manhattan", viene ignorato se x è
una matrice di dissimilarità |
|
stand |
T (true) se si vuole standardizzare i dati
prima di procedere al calcolo della matrice
di dissimilarità, in alternativa
F (false), viene ignorato se x è
una matrice di dissimilarità |
tess.fan <- funny(tess.dis, 3, diss=T)
Un oggetto fanny
ha le seguenti proprietà:
|
objective |
fornisce il valore della funzione obiettivo
al termine delle iterazioni ed il numero
di iterazioni richieste per ottenere il
valore minimo |
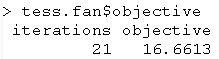
|
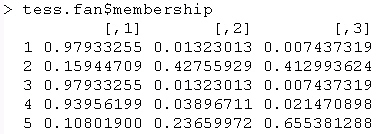
membership |
matrice contenente il coefficiente di appartenenza
di ogni punto ad ogni cluster |
.....

|
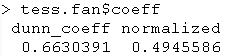
coeff |
coefficiente di Dunn, sia nella versione
normale sia in quella standardizzata |
|
clustering |
vettore
con il nearest crisp clustering per
ciascuna unità, ovvero il gruppo
di appartenenza più vicino, ovvero
ogni oggetto i viene assegnato al cluster
v per il
quale ha il più alto coefficiente
di appartenenza |

|
silinfo |
elenco di tutte le informazioni necessarie
per costruire il silhouette plot relativamente
nearest crisp clustering; nella prima
parte è riportato per ogni oggetto
il cluster di appartenenza, quello più
vicino e la silhouette width, sono
poi visualizzati la media per gruppo e la
media complessiva. |

……
Anche per la procedura fanny
vengono prodotti due output grafici, il silhouette
plot ed il cluster plot.
plot(tess.fan)
Come si può osservare
vi è differenza tra i gruppi identificati
precedentemente con pam
e quelli ottenuti con fanny.
In particolare la diversificazione
si registra nel gruppo 2 ottenuto con fanny

Più in dettaglio si
può osservare che 2 unità classificate
nel gruppo 1 con pam
cadono invece nel gruppo 2 secondo il metodo dei
nearest crisp clustering di fanny
(che corrisponde alla cluster 3 secondo la partizione
pam).
Come si può notare dalla tabella seguente
sono unità per le quali il miglior vicino
è il cluster 3, che presentano coefficienti
di appartenenza molto vicini ed inoltre forniscono
i valori più bassi di silhouette width
all'interno del loro gruppo.
| RowNames |
cluster
pam |
neighbor
pam |
sil_width
pam |
Coefficiente
appartenenza fanny |
|
|
|
|
Clust_1 |
Clust_2 |
Clust_3 |
| 51 |
1 |
3 |
0.25 |
0.37 |
0.38 |
0.25 |
| 309 |
1 |
3 |
0.25 |
0.37 |
0.38 |
0.25 |
Vi sono altri 15 casi classificati
nel gruppo 2 secondo il metodo dei k-medoids,
che ricadono invece nel cluster 2 secondo fanny
(corrispondente sempre al cluster 3 pam).
Anche in questo caso si tratti di unità
particolarmente "sfumate", la loro appartenenza
al gruppo 2, secondo la silhouette width, è
molto bassa ed il coefficiente di appartenenza
ai due cluster in esame è sostanzialmente
simile, oltre a presentare valori significativi
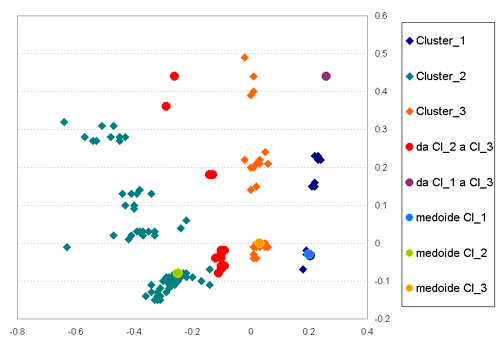
Anche dal grafico seguente si può osservare
come questi 15 casi (marcati in rosso) si trovino
in una situazione intermedia tra i due gruppi.
| RowNames |
cluster
pam |
neighbor
pam |
sil_width
pam |
Coefficiente
appartenenza fanny |
|
|
|
|
Clust_1 |
Clust_2 |
Clust_3 |
| 2 |
2 |
3 |
0.11 |
0.16 |
0.43 |
0.41 |
| 61 |
2 |
3 |
0.03 |
0.16 |
0.44 |
0.4 |
| 97 |
2 |
3 |
0.01 |
0.19 |
0.44 |
0.38 |
| 98 |
2 |
3 |
0.03 |
0.15 |
0.44 |
0.4 |
| 99 |
2 |
3 |
0.02 |
0.18 |
0.44 |
0.38 |
| 102 |
2 |
3 |
0.01 |
0.17 |
0.44 |
0.39 |
| 110 |
2 |
3 |
0.06 |
0.18 |
0.43 |
0.4 |
| 113 |
2 |
3 |
0.09 |
0.22 |
0.4 |
0.38 |
| 178 |
2 |
3 |
0.07 |
0.18 |
0.41 |
0.41 |
| 230 |
2 |
3 |
0.13 |
0.2 |
0.41 |
0.39 |
| 238 |
2 |
3 |
0.08 |
0.16 |
0.42 |
0.41 |
| 242 |
2 |
3 |
0.06 |
0.15 |
0.45 |
0.4 |
| 291 |
2 |
3 |
0.05 |
0.15 |
0.45 |
0.4 |
| 344 |
2 |
3 |
0.04 |
0.16 |
0.45 |
0.39 |
| 346 |
2 |
3 |
0.07 |
0.16 |
0.44 |
0.4 |
|