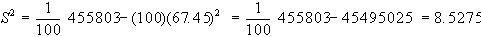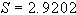Manuale di statistica descrittiva

 

INTRODUZIONE *

STATISTICA DESCRITTIVA *

1. Classificazione *
2. Distribuzioni di frequenze *
3. Rappresentazioni grafiche *
4. Valori medi *
5. Misure di variabilità o dispersione *

 

 

 

 

INTRODUZIONE

 

 

 

E' difficile dare una definizione esaustiva di statistica, in termini molto generali si può dire che si tratta di un insieme di metodi aventi per oggetto lo studio di fenomeni collettivi.

Si tratta cioè di una varietà di tecniche, ognuna con finalità diverse, volte ad analizzare un insieme di valori risultanti dall'osservazione di un fenomeno collettivo caratterizzato da una certa variabilità.

Il contesto è quindi sempre costituito da un insieme di unità dotate di uno o più caratteristiche comuni. L'obiettivo è quello di passare dal caso individuale all'insieme dei casi, alla ricerca di leggi dell'insieme, e questo a causa della variabilità dei fenomeni collettivi.

Un esempio può risultare utile per chiarire questi concetti. Se consideriamo la produzione di bulloni da parte di una macchina, per quanto possa essere precisa la macchina, dovremo aspettarci che ogni pezzo differisca dagli altri rispetto ad una caratteristica a cui possiamo essere interessati, ad esempio il diametro. Abbiamo cioè un collettivo costituito dalla produzione di bulloni, un carattere comune a tutte le unità di tale collettivo rappresentata dal diametro. Questo carattere sarà in ogni caso caratterizzato da una variabilità, ovvero da una naturale diversità fra le unità.

Il primo obiettivo che si pone la statistica è quello di sintetizzare le informazioni raccolte per ogni unità riguardo al carattere a cui si è interessati per individuare una legge generalmente valida sul comportamento di tale carattere nel collettivo in esame. Nell'esempio dei bulloni si può quindi essere interessati a determinare se la produzione deve essere ritenuta conforme a delle specifiche fissate in fase di progettazione della macchina.

Il problema che si pone nella maggioranza dei casi pratici è rappresentato dalla difficoltà di osservare tutte le unità di un determinato collettivo. Dato ad esempio un lotto di 10000 bulloni, può infatti risultare dispendioso, in termini di tempo e quindi economici, misurare il diametro di tutti i pezzi del lotto per verificarne la qualità. Si dovrà quindi osservare una parte di tale lotto, e, sulla base di questa osservazione parziale, decidere se il lotto può essere ritenuto "soddisfacente". 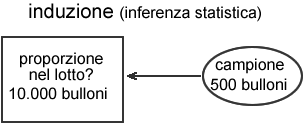Questo è un tipico esempio di inferenza statistica, poichè le caratteristiche del collettivo, il lotto, sono indotte da quelle di un suo sottoinsieme, detto campione. Si dovranno perciò inizialmente sintetizzare le informazioni del campione per mezzo di metodi di statistica descrittiva, per poi indurle per l'intera popolazione.

Abbiamo quindi due insiemi di tecniche statistiche: quelle di tipo descrittivo che hanno la finalità di sintetizzare un insieme di osservazioni riguardanti uno o più caratteri comuni alle unità di un collettivo, o di una parte di un collettivo; quelle di tipo induttivo che si prefiggono lo scopo di individuare le modalità per una corretta selezione di un sottoinsieme di un collettivo e le descrizione di quest'ultimo attraverso una sua osservazione parziale. Nella prima parte di questa dispensa verranno presentati alcuni strumenti di statistica descrittiva, quali la classificazione, le medie e le misure di variabilità. Nella seconda parte verranno invece presi in considerazione tutti gli aspetti concernenti l'induzione statistica. A questo riguardo si deve sottolineare che, prima di affrontare in specifico le modalità attraverso cui effettuare inferenza su una popolazione partendo da un campione, va affrontato il problema di come, data una popolazione, si ottiene un campione che possa essere utilizzato per studiare la popolazione da cui è tratto.

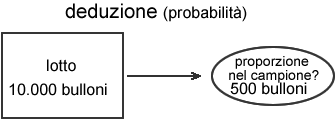
In altri termini saremo principalmente interessati ad una argomentazione induttiva: cioè che un carattere della popolazione può essere indotto dall'osservazione di un campione, ma questa argomentazione si basa su una deduzione a priori: il carattere osservato nel campione molto probabilmente è vicino a quello della popolazione.

Ritorniamo all'esempio del lotto i 10000 bulloni, e supponiamo ad esempio di essere interessati alla proporzione di pezzi difettosi presenti in tale lotto. In pratica noi osserveremo un campione (ad esempio di 500 bulloni) tratto da questo lotto e, sulla base della proporzione registrata nel campione, riterremo che la proporzione di difettosi nel lotto sia pari a quella campionaria, più o meno un certo errore, derivante dalla situazione di informazione connessa al fatto di avere osservato solo una parte della popolazione.

In realtà il problema che sta a monte di questo procedimento inferenziale è rappresentato da: con quale probabilità avrò un campione rappresentativo della popolazione che debbo studiare? In altri termini il fatto di ritenere la proporzione di difettosi calcolata sui 500 bulloni, rappresentativa di quella dei 10000 bulloni, si basa sul fatto che ritengo molto probabile che la proporzione di difettosi nel campione sia vicina a quella del lotto.

 

I primi capitoli della seconda parte della dispensa sono quindi dedicati alla deduzione, in particolare allo studio della probabilità, delle variabili casuali, delle loro distribuzioni caratteristiche e del problema del campionamento. In breve ci chiederemo; "data una certa popolazione, come si comporterà un campione tratto da essa? Sarà rappresentativo?". Solo quando saranno risulti questi problemi di deduzione potremo affrontare quelli di induzione. Si cercherà quindi di rispondere alla seguente domanda: "con quale precisione potremo compiere inferenze sulla popolazione ignota partendo da un campione osservato?". Individueremo, in primo luogo, il modo per fornire una stima di un parametro della popolazione partendo da un campione e, in secondo luogo, le modalità per verificare delle ipotesi su un parametro della popolazione, partendo sempre dal campione.

 

 

 

STATISTICA DESCRITTIVA

 

1. Classificazione

Un primo passaggio per giungere ad una sintesi delle osservazioni consiste nella loro classificazione; questa darà luogo ai dati statistici.

Ogni tipo di classificazione riflette un'ipotesi di lavoro, anche se provvisoria.

Il momento classificatorio è alla base di tutte le scienze di osservazione (fisiche, biologiche, sociali) e permette una schematizzazione di una realtà complessa e prepara il passaggio alle quantità.

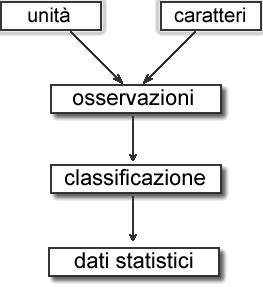
La classificazione si risolve nella convenzionale riduzione di una pluralità di oggetti in due o più categorie (classi) mutuamente escludentisi. Questo impone la scelta di un criterio discriminante per la costruzione delle classi; tale criterio sarà evidentemente dettato da quelli che sono gli obiettivi conoscitivi.

Innanzitutto sono da distinguere diversi tipi di dati derivanti dall'osservazione dei caratteri delle unità:

caratteri di tipo quantitativo esprimibili con una misura (statura, peso, diametro, ecc.) su un continuo, oppure discreti, che assumono cioè solo determinati valori (numero di pezzi difettosi, numero di difetti in una unità, numero di pezzi prodotti, ecc.)

caratteri di tipo qualitativo, per i quali non è prevedibile un ordinamento (sesso, religione, difettoso/non difettoso, ecc.).

In base al tipo di dati osservati è possibile definire diversi tipi di classificazione:

1.scale nominali: livello più basso di misurazione; in esse si attribuiscono dei nomi alle varie classi, in modo arbitrario, senza che questo implichi una relazione di merito tra le classi stesse. Un esempio di classificazione di questo tipo è il sesso di un gruppo di persone osservate: non è infatti un carattere misurabile, e l'ordinamento della classificazione in maschio-femmina o femmina-maschio non implica alcun cambiamento nella classificazione stessa.

2.scale ordinali: quando è possibile ordinare le classi in base ad una certa caratteristica senza che però sia possibile precisare quanta ne posseggono. Ad esempio il titolo di studio, in questo caso possiamo dire che una classe è maggiore di un'altra, ma non abbiamo alcuna informazione sulla grandezza della differenza tra gli elementi.

3.scale ad intervalli: derivanti da grandezze misurabili (diametro, peso, ore lavorate, reddito, ecc.), possiamo ordinare le unità in relazione al fatto che possiedano in misura maggiore o minore una determinata caratteristica e possiamo inoltre indicare l'esatta distanza tra essi.

La formazione di classi traduce la pluralità di valori osservati in una distribuzione statistica. Possiamo quindi dare che una prima rappresentazione sintetica delle informazioni raccolte tramite delle tavole statistiche.

Se abbiamo perciò n individui osservati, in cui il carattere ordinatore X assume i valori 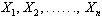e assunti m livelli (o intervalli) di X, con Mn (m classi), avremo che:

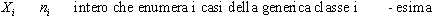
è una distribuzione statistica.

 

2. Distribuzioni di frequenze

Quando si hanno grandi quantità di dati grezzi (osservazioni elementari) è spesso utile distribuire i dati stessi in classi e determinare il numero di individui che appartiene a ciascuna classe. Questo numero è detto frequenza assoluta della classe.

L'ordinamento in una tavola di tutte le classi con le rispettive frequenze è detta distribuzione di frequenze.

Esempio 1:

diametro in mm.	numero di casi
60-62	5
63-65	18
66-68	42
69-71	27
72-74	8
totale	100

I valori 60-62 sono detti limiti della classe (rispettivamente limite inferiore e superiore).

In questo esempio se i diametri sono registrati al mm più prossimo, l'intervallo della classe 60.62 comprende tutti i diametri da 59.5 a 62.5: questi due valori sono detti limiti reali della classe o confini della classe.

L'ampiezza dell'intervallo è data dalla differenza tra confine superiore ed inferiore (62.5-59.5=3).

Il valore centrale si ottiene sommando il limite inferiore e quello superiore e dividendo per due ( (60+62)/2=61 ).

La frequenza relativa di una classe è la frequenza assoluta della rapportata al totale delle osservazioni (freq. relativa della prima classe pari a 5/100=0.05). La tavola che si ottiene utilizzando le frequenze relative è detta distribuzione delle frequenze relative. Spesso le frequenze relative sono espresse in termini percentuali: questo esprime il numero di osservazioni che si avrebbero in una classe se il numero totale di osservazioni fosse di 100 unità.

La frequenza totale di tutti i valori inferiori al confine superiore di una classe è detta frequenza cumulata. Ad esempio per la classe 66-68, la freq. cumulata è pari a 5+18+42=65, cioè 65 pezzi hanno un diametro inferiore a 68.5 mm.

diametro in mm.	frequenza assoluta	frequenza relativa	frequenza assoluta cumulata	frequenza relativa cumulata
60-62	5	0.05	5	0.05
63-65	18	0.18	23	0.23
66-68	42	0.42	65	0.65
69-71	27	0.27	92	0.92
72-74	8	0.08	100	1
totale	100	1

 

 

 

 

 

 

3. Rappresentazioni grafiche

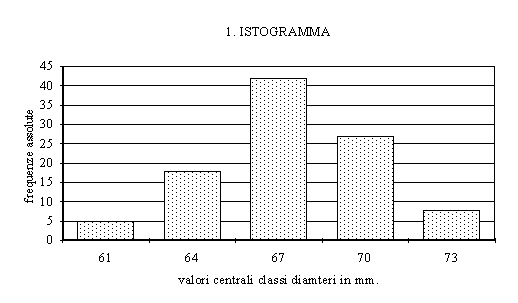
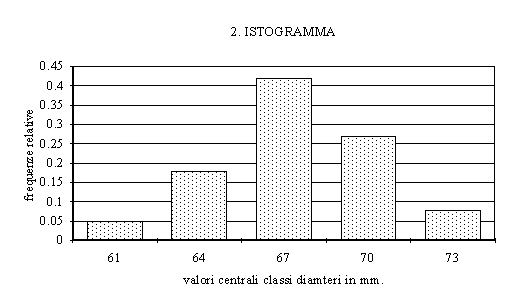
Il modo più immediato per rendere graficamente una distribuzione di frequenze consiste nella costruzione di un istogramma. Si tratta di un grafico composto da tanti rettangoli quante sono le classi della distribuzione, ognuno con una altezza pari alla frequenza della classe (la frequenza può essere quella assoluta o, in alternativa, quella relativa).

 

 

 

 

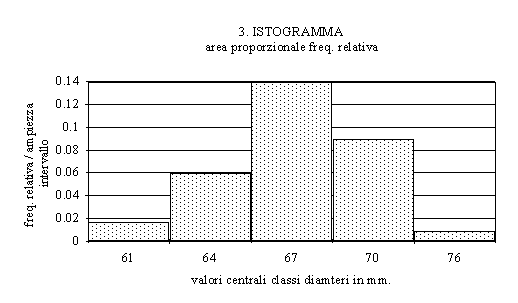
E' possibile costruire istogrammi in cui sia l'area ad essere proporzionale alla frequenza relativa. L'utilità di questo tipo di istogramma consiste nella possibilità di rappresentare correttamente anche classificazioni in cui l'ampiezza degli intervalli non è uguale per tutte le classi.

 

 

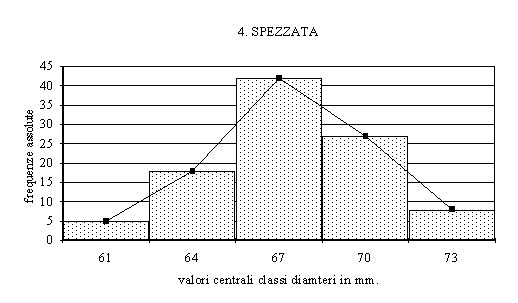
Si dicono spezzate quei grafici in cui il valore centrale di ciascuna classe è congiunto a quello delle classi vicine appunto per mezzo di una spezzata:

 

 

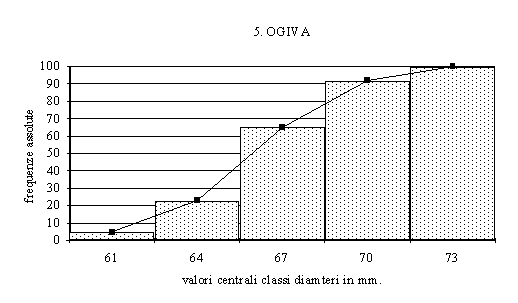
Vengono invece dette ogive le rappresentazioni grafiche delle distribuzioni cumulate di frequenza:

 

 

Oltre agli istogrammi e alle spezzate è possibile rendere visivamente distribuzioni per mezzo di altri tipi di grafico, quali le torte o le pile.

Le torte sono costitute da un cerchio la cui area è suddivisa in spicchi proporzionali alle diverse classi della distribuzione da rappresentare. L'area complessiva della torta rappresenta quindi la totalità delle osservazioni, mentre ciascuna fetta rappresenta il peso percentuale di ciascuna classe.

 

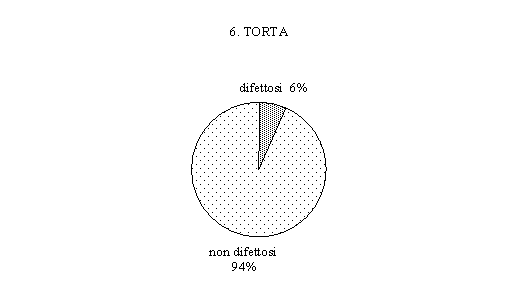
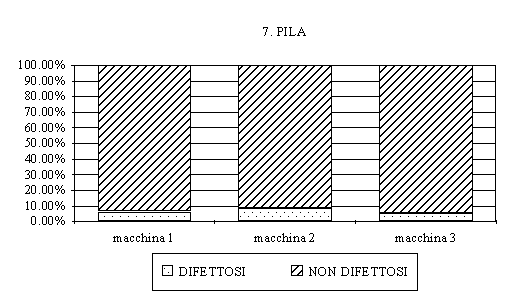
Le pile sono grafici concettualmente simili alle torte, con la differenza che, anzichè fare riferimento ad un cerchio, la totalità delle osservazioni è rappresentata da un rettangolo la cui area è suddivisa proporzionalmente tra le varie classi.

 

 

4. Valori medi

Affrontiamo ora il problema di come si possa caratterizzare una distribuzione di frequenze o una serie di osservazioni, per mezzo di una singola misura descrittiva. In realtà si tratta di individuare due tipi di descrizione molto utili: la prima è costituita dal punto centrale o valore medio, la seconda dalla dispersione o misura di variabilità.

Vi possono essere diverse misure del valore medio; la prima e più semplice è costituita dalla moda, che in una distribuzione di frequenze è rappresentata dal valore centrale della classe più numerosa. Questa misura non può essere considerata sufficiente per descrivere in sintesi una classificazione, dipende infatti dal raggruppamento arbitrario di dati.

La misura di intensità più comunemente utilizzata è la media aritmetica. Questa rappresenta l'ammontare del carattere che spetterebbe a ciascuna unità se il carattere fosse distribuito uniformemente.

Nel caso di osservazioni elementari la media aritmetica si calcola come somma dell'ammontare del carattere in ciascuna unità, e dividendo tale somma per il numero di unità che hanno contribuito a tale somma:

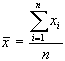
Esempio 1:

osservazioni: spessore in cm. 12.5 13.2 12.7 13.0 13.1 12.4

somma osservazioni= 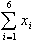= 12.5+13.2+12.7+13.0+13.1+12.4= 76.9

media 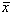=76.9/6=12.82

Nel caso invece che si abbiano dei dati già classificati in una distribuzione di frequenze, non sarà più possibile sommare l'ammontare del carattere in ciascuna unità perchè, per mezzo della classificazione, si è già perso il riferimento alle singole unità; si deve quindi ricorrere all'ipotesi che ciascuna unità appartenente ad una classe disponga di una quantità del carattere pari al punto centrale della classe a cui appartiene. In altri termini, ritornando all'esempio dei diametri, non sappiamo quali siano le misure dei diametri dei 5 pezzi che ricadono nella prima classe; dovremo quindi porre l'ipotesi che tutti e 5 abbiano un diametro pari a 61 mm (valore centrale di quella classe). A questo punto per ricostruire l'ammontare complessivo del carattere in tutte le unità osservate, si dovrà sommare il prodotto tra il valore centrale per la frequenza assoluta per tutte le classi, e dividere per il numero totale di unità:

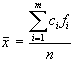
dove:

 

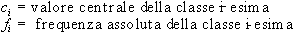
Esempio 2:

classificazione diametri in mm.

diametro in mm.	numero di casi	valori centrali delle classi
60-62	5	61
63-65	18	64
66-68	42	67
69-71	27	70
72-74	8	73
totale	100

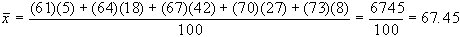
Una terza misura di intensità è rappresentata dalla mediana. Si tratta del cinquantesimo percentile, ovvero del valore al di sotto del quale cade la metà dei valori osservati.

Nel caso quindi di osservazioni elementari non si dovrà fare altro che ordinare in modo crescente le osservazioni e verificare quale sia il valore centrale, nel caso in cui il numero di osservazioni sia dispari; se le osservazioni sono pari si dovrà invece considerare la semisomma dei due valori centrali:

osservazioni ordinate	osservazioni ordinate
2	2
5	5
7	7
11	11
12	12
	15
mediana=7	mediana=(7+11)/2=9

Se invece si dispone di una distribuzione di frequenze la procedura di calcolo della mediana diviene:

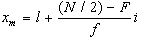
dove:

l=confine superiore della classe contenente la mediana

F=frequenza cumulata corrispondente al limite inferiore della classe contenente la mediana

f=frequenza assoluta della classe contenente la mediana

i=ampiezza della classe contenente la mediana.

Esempio 3:

Riprendendo la distribuzione dell'esempio precedente abbiamo:

diametro in mm.	frequenza assoluta	frequenza assoluta cumulata
60-62	5	5
63-65	18	23
66-68	42	65
69-71	27	92
72-74	8	100
totale	100

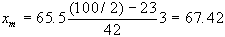
5. Misure di variabilità o dispersione

Benchè la media possa essere la più importante caratteristica in una popolazione o in un campione è altrettanto importante conoscere come si dispongono le unità osservate. Come nel caso delle misure medie, vi sono parecchie misure di dispersione.

La più semplice è costituita dal campo di variazione, calcolata come distanza tra il valore più grande e quello più piccolo.

Se consideriamo le osservazioni dello spessore in cm. di un bullone:

[12.5, 13.2, 12.7, 13.0, 13.1, 12.4]

il campo di variazione sarà: 13.2-12.4=0.8cm.

Questo tipo di indice va incontro ad una critica immediata, poichè non dice nient'altro della distribuzione se non i suoi limiti. Questi due valori (il massimo e il minimo) possono anche non essere particolarmente significativi; per questo motivo si preferisce utilizzare indici di variabilità che tengano conto di tutte le osservazioni.

Lo scarto medio si trova calcolando la differenza di ciascuna osservazione dalla media, facendo poi una media aritmetica di questi scarti 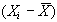. Benchè questa possa essere considerata una buona misura di variabilità, sorge il problema che la somma degli scarti positivi annulla la somma degli scarti negativi, dando quindi sempre luogo ad una media nulla. Per ovviare a questo problema una prima soluzione consiste nel calcolare la media degli scarti in valore assoluto; dando luogo allo scarto medio assoluto:

Questa rappresenta una buona misura di variabilità, tuttavia presenta alcuni inconvenienti dal punto di vista matematico. Si preferisce quindi un indice alternativo che supera il problema del segno degli scarti, elevando al quadrato ogni scarto: la varianza:

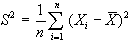
Una formula calcolatoria che consente di ottenere il valore della varianza in maniera più rapida è costituita da:

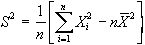
La varianza esprime la variabilità delle osservazioni nell'unità di misura delle osservazioni stesse elevata al quadrato; per ottenere una misura di dispersione che abbia invece la stessa unità di misura osservata si calcola lo scarto quadratico medio o deviazione standard:

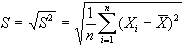
la quale non è altro che la radice quadrata della varianza.

Le formule viste per la varianza e lo scarto quadratico medio sono valide nel caso in cui si disponga di dati elementari; se invece sono disponibili dati raggruppati in classi dovremo ancora una volta ipotizzare che tutte le osservazioni che ricadono in una determinata classe presentino una intensità del carattere pari al valore centrale della classe. Avremo perciò che la varianza sarà:

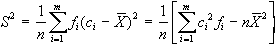
dove: c rappresenta il valore centrale delle classi e f la frequenza assoluta.

Anche per dati raggruppati in classi la deviazione standard sarà pari alla radice quadrata della varianza.

Esempio 1

Riprendiamo le osservazioni: spessore in cm. 12.5 13.2 12.7 13.0 13.1 12.4

in questo caso la media è pari a 12.82, per cui la varianza sarà:

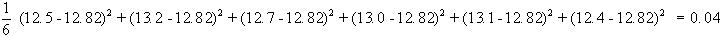lo stesso risultato si può ottenere con la formula calcolatoria:

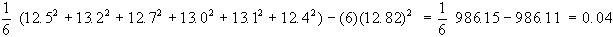
lo scarto quadratico medio sarà quindi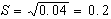

Esempio 2

consideriamo nuovamente la distribuzione:

diametro in mm.	frequenza assoluta f	valori centrali c	valori centrali al quadrato per frequenza assoluta c2f
60-62	5	61	3721*5=18605
63-65	18	64	4096*18=73728
66-68	42	67	4489*42=188538
69-71	27	70	4900*27=132300
72-74	8	73	5329*8=42632
totale	100		455803