| Manuale
introduttivo all'inferenza statistica |
|
PROBABILITÀ *
1.
Definizione di probabilità e sue proprietà
elementari *
2. Eventi e loro probabilità *
2.1 Spazio degli eventi *
2.2 Eventi *
2.3 Combinazione di eventi *
2.4 Probabilità di eventi derivati *
2.5 Eventi condizionati *
2.6 Indipendenza *
VARIABILI
CASUALI *
1.
Definizione di variabili casuali *
2. Variabili casuali discrete *
3. Variabili casuali continue *
4. Distribuzioni di probabilità congiunte *
5. Parametri delle distribuzioni di probabilità *
5.1 Valore medio di una variabile casuale *
5.2 Misure di variabilità *
5.3 Momenti delle distribuzioni congiunte *
MODELLI
DISTRIBUTIVI *
1.
Modelli distributivi discreti *
1.1 Modello di Bernoulli *
1.2 Modello Binomiale *
1.3 Modello ipergeometrico *
1.4 Modello di Poisson *
2. Modelli distributivi continui *
2.1 Modello normale o gaussiano *
CAMPIONAMENTO
E DISTRIBUZIONI CAMPIONARIE *
1.
Popolazione e campione *
2. Il campione casuale *
3. Distribuzione campionaria delle medie *
4. Distribuzione campionaria del numero di successi e
della proporzione *
STIMA
DEI PARAMETRI *
1.
Stima per intervalli *
2. Intervalli di confidenza per la media *
3. Intervalli di confidenza per una proporzione *
VERIFICA
DELLE IPOTESI *
1.
Controllo di ipotesi sulla media di una popolazione *
1.1 Test bilaterale *
1.2 Test unilaterale *
1.3 Determinazione della numerosità campionaria
fissati e *
1.4 Test di ipotesi per la media nel caso di ignota *
2. Controllo di ipotesi sulla proporzione di una popolazione *
PROBABILITÀ
Nei capitoli che
seguono verranno effettuate deduzioni riguardo ad un campione
estratto da una popolazione nota. Questo studio è
preliminare all'induzione, della quale si tratterà
in seguito partendo da un campione noto per compiere inferenze
su una popolazione ignota.
Se la produzione
di una macchina utensile presentasse una difettosità
pari al 2%, non potremo mai essere sicuri che, in un campione
casuale, si troverà esattamente la stessa percentuale
di pezzi difettosi; tuttavia è probabile che
la percentuale osservata nel campione sia vicina a
quella della popolazione. Si tratta quindi di chiarire i
vocaboli probabile e vicina a in modo più
preciso, si tratta in altri termini di definire le leggi
probabilistiche che stanno alla base delle previsioni in
condizioni di incertezza.
1.
Definizione di probabilità e sue proprietà
elementari
Se consideriamo
il caso del lancio di un dado, cerchiamo di definire la
probabilità che esca la faccia 1. Intuitivamente,
dal momento che questo è uno dei sei eventi equiprobabili,
potremo arguire che la probabilità sia pari ad un
sesto. In altre parole, potremo dire che, se il dado venisse
lanciato un gran numero di volte, la frequenza relativa
della faccia 1 si approssimerebbe a un sesto. Questa definizione
di probabilità come frequenza relativa limite è
formalmente stabilita dalla:
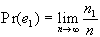
in cui e1
è l'evento, n è il numero totale delle volte
in cui l'esperimento viene ripetuto (lancio del dado), n1
è il numero delle volte che si verifica l'evento
e1
(frequenza f di e1);
n1/n
è perciò la frequenza relativa di e1.
Generalizzando,
se un esperimento è costituito da N eventi elementari
(e1,e2,....,ei,....eN),
le frequenze relative ni/n
di ogni evento ei
saranno positive, dal momento che sia il numeratore che
il denominatore sono positivi; inoltre siccome il numeratore
risulta non superiore del denominatore, la frequenza relativa
non può essere superiore ad 1. Pertanto:
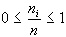
e poichè la stessa
relazione è valida al limite, si avrà:

Inoltre, si deve osservare
che siccome tutti i possibili eventi hanno per somma n
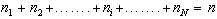
dividendo questa equazione
per n otteniamo che tutte le frequenze relative hanno per
somma l'unità:
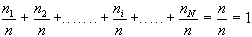
2.
Eventi e loro probabilità
2.1
Spazio degli eventi
Supponiamo che l'esperimento
consista nel lancio di una moneta per tre volte. L'elenco
di tutti i possibili risultati, cioè di tutti i possibili
eventi sarà:
T T T =e1
T T C =e2
T C T =e3
T C C =e4
C T T =e5
C T C =e6
C C T =e7
C C C =e8
L'insieme dei risultati
è detto Spazio campione S.
Ognuno degli otto possibili
eventi elementari avrà una probailità di 1/8.
2.2
Eventi
Continuando con
l'esempio del lancio della moneta per tre volte, definiamo
l'evento
E: almeno 2 Teste
questo evento comprende
i punti campione e1 e2
e3
e5
, diremo pertanto che l'evento E è l'insieme dei
punti {e1 e2
e3
e5
}
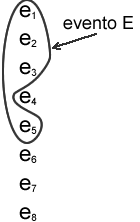
Un evento E è
un sottoinsieme dello spazio campione S. La sua probabilità
sarà data da:
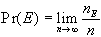
in cui nE
è la frequenza di E. Naturalmente E si presenta ogni
volta che si presentano i punti campione e1
e2
e3
e5
e quindi:
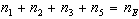
per cui si ottiene:
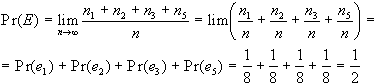
La generalizzazione
di quanto riportato sopra è che la probabilità
di un evento è la somma delle probabilità
di tutti i punti campione (o eventi elementari) compresi
in quell'evento, vale a dire:
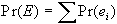
Nella tabella che
segue sono riportati diversi eventi; come è immediato
notare nella colonna (3) sono riportati tutti gli eventi
elementari compresi in ogni evento:
Tavola 1
| Simbolo
arbitrario
per l'evento
(1) |
Descrizione
(2) |
elenco
dei
punti campione
(3) |
probabilità
(4) |
| E |
almeno
2 teste |
e1
e2 e3 e5 |
1/8+1/8+1/8+1/8=1/2 |
| F |
seconda
moneta testa seguita da croce |
e2
e6 |
1/4 |
| G |
meno
di 2 teste |
e4
e6 e7 e8 |
1/2 |
| H |
stesso
risultato |
e1
e8 |
1/4 |
| I |
nessuna
testa |
e8 |
1/8 |
| I1 |
1
testa |
e4
e6 e7 |
3/8 |
| I2 |
2
teste |
e2
e3 e5 |
3/8 |
| I3 |
3
teste |
e1
|
1/8 |
| J |
meno
di 2 croci |
e1
e2 e3 e5 |
4/8 |
2.3
Combinazione di eventi
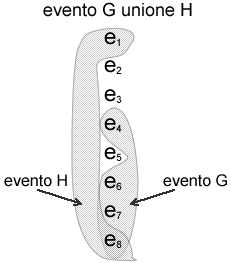
Se consideriamo
i due eventi G ed H potremo ricercare la probabilità
di ottenere meno di due teste o che tutte le monete presentino
la stessa faccia, cioè la probabilità di <G
o H>. Questo evento congiunto si indica con <GH>
(G unione H). Dalla tavola 1 si vede che l'evento unione
tra G ed H è dato da:
GH = {e4
e6
e7
e8
e1}
In altri termini definiamo
GH l'insieme di tutti i punti campione che sono in G o in
H o in entrambi.
In questo esempio, poichè
in GH sono compresi 5 degli 8 punti equiprobabili, la sua
probabilità sarà di 5/8.
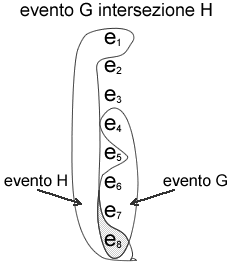
Analogamente potremo
essere interessati all'evento <G e H>, cioè
che si verifichino meno di due teste e che tutte le monete
presentino la stessa faccia. Tale evento viene indicato
con GH (G intersezione H). L'unico punto in comune tra gli
eventi G ed H è rappresentato da {e8}
GH={e8}
ne segue che la probabilità
di GH risulta pari ad 1/8. In generale, per ogni coppia
di eventi G ed H, definiamo GH come l'insieme dei punti
che sono in G ed in H.
2.4
Probabilità di eventi derivati
Se consideriamo una coppia di eventi
che non abbiano nessun punto in comune, come gli eventi
I e J della tabella 1, si può facilmente osservare
che:
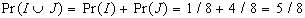
Questa semplice
somma non è comunque sempre valida, infatti:
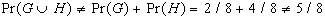
La differenza è
dovuta al fatto che G ed H si sovrappongono e che quindi
nel sommare Pr(G) e Pr(H) teniamo conto due volte dell'intersezione
GH. Potremo quindi scrivere correttamente che:
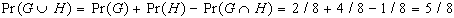
Nel caso degli eventi
I e J abbiamo che la loro intersezione è vuota Pr(IJ)=0,
per cui:
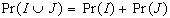
Più eventi
si dicono mutuamente incompatibili se nessuno si sovrappone
all'altro, cioè se nessun evento elementare appartiene
a più di un solo evento.
Nella tabella 1
gli eventi I, I1,I2
si escludono a vicenda, mentre ciò non accade per
gli eventi E, F ed I.
In particolare
gli eventi I, I1,I2,I3
si escludono a vicenda e la loro unione "copre" l'intero
spazio campione: in questo caso si parla di partizione
di S.
2.5
Eventi condizionati
Definiamo la probabilità
condizionata affermando che se G ed H sono due eventi dello
spazio campione S e Pr(G)>0, allora la probabilità
condizionata di H, dato G, Pr(H/G), è:
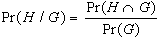
Facendo sempre riferimento
agli eventi definiti nella tabella 1, si supponga che sia
stato effettuato un lancio della moneta per tre volte e
di essere informati del fatto che si sono verificate meno
di due teste, cioè che si è verificato l'evento
G; sotto questa condizione ci si chiede quale sia la probabilità
che sia avvenuto l'evento H (monete tutte uguali).
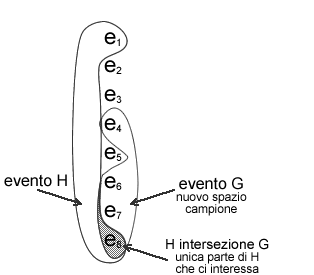
Determinare la probabilità
di H, dato G, equivale a determinare la probabilità
di H relativamente allo spazio campione G: i soli elementi
di H che interessano sono quelli che appartengono pure a
G, ossia i punti campione dell'insieme GH.
Partendo dalla definizione
di probabilità condizionata si ottiene:
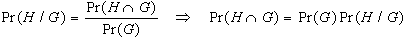
2.6
Indipendenza
Definiamo come indipendenti
due eventi A e B quando:
Pr(A/B)=Pr(A) e quindi
se Pr(AB)=Pr(A)Pr(B).
In altri termini significa
che il fatto di disporre di informazioni sul verificarsi
dell'evento B non modifica la probabilità dell'evento
A.
Se ad esempio definiamo
tre eventi, sempre in riferimento al lancio della moneta
tre volte:
E1:
i primi due lanci presentano testa {e1
e2}
= 2/8=1/4
E2:
l'ultimo presenta testa {e1
e3
e5
e7}=4/8=1/2
E3:
tutti i lanci presentano testa {e1}=1/8
potremo affermare che
E1
e E2
sono indipendenti, infatti
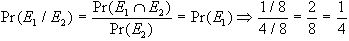
mentre E1
e E3
non sono indipendenti, infatti:
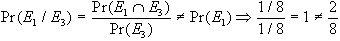
VARIABILI
CASUALI
1.
Definizione di variabili casuali
Considerando nuovamente
l'esperimento del lancio della moneta per tre volte, si
associ ad ogni evento elementare dello spazio campione il
corrispondente numero di teste, che indichiamo con X. In
questo modo si definisce una variabile, il cui singolo valore,
che corrisponde ad un sottoinsieme dello spazio campione,
è esso stesso un evento. L'insieme dei valori di
X costituisce uno spazio campione numerico su cui può
essere definita una misura di probabilità, come illustrato
nella figura seguente:
eventi elementari X
e1 T
T T 3 valori di X Probabilità
e2 T
T C 2
e3 T
C T 2 0 1/8
e4 T
C C 1 1 3/8
e5 C
T T 2 2 3/8
e6 C
T C 1 3 1/8
e7 C
C T 1
e8 C
C C 0 totale 1
In generale si definisce
variabile casuale una funzione che associa ad ogni
evento elementare e dello spazio campione S uno ed
un solo numero reale.
Associando ad ogni
possibile valore di X la sua probabilità, come somma
delle probabilità degli eventi elementari che forniscono
quel determinato valore di X, si ottiene la distribuzione
di probabilità della variabile casuale X.
In termini generali
se l'insieme di eventi {A1,A2
A3
..... An
} definiti su uno spazio campione costituiscono un insieme
esaustivo di eventi mutuamente escludentisi (dove A1,A2
A3
..... An
rappresentano i possibili valori della variabile casuale
X) il corrispondente insieme di valori di probabilità
associato agli eventi in questione {Pr(A1),Pr(A2),
Pr(A3).....
Pr(An)}
costituisce una distribuzione di probabilità.
2.
Variabili casuali discrete
La variabile casuale
X si chiama discreta se è definita in uno
spazio campionario discreto; potrà quindi assumere
un numero finito o un'infinità numerabile di valori.
Sono discrete, ad esempio, le variabili: numero di pezzi
difettosi prodotti da una macchina; numero di elementi non
difettosi osservati fino al primo difettoso.
Nel caso di una
v.c. discreta che assuma n valori x1,x2
..... xn
dovranno essere soddisfatte le condizioni:
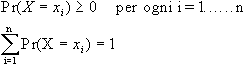
la funzione p(xi)=Pr(X=xi)
si dice funzione di massa di probabilità (FMP)
mentre la funzione 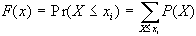 viene denominata funzione cumulativa di distribuzione
(FCD) o funzione di ripartizione e rappresenta la
probabilità che la v.c. X assuma valori inferiori
ad un certo valore x di X.
viene denominata funzione cumulativa di distribuzione
(FCD) o funzione di ripartizione e rappresenta la
probabilità che la v.c. X assuma valori inferiori
ad un certo valore x di X.
3.
Variabili casuali continue
Una variabile casuale
X si dice continua se è definita in uno spazio campionario
continuo, essa può quindi assumere tutti i valori
di un certo intervallo. Sono continue variabili come il
diametro di un bullone prodotto da una certa macchina, la
temperatura registrata in un ambiente, e così via.
Si noti che la v.c.
continua è solo un'astrazione: essa non è
osservabile nella realtà. Se consideriamo infatti
il diametro di un bullone, comunque si fissino due suoi
valori, esso potrà assumere qualunque valore intermedio.
Tuttavia nella realtà la traduzione in cifre dell'osservazione
dà luogo ad un insieme discreto di numeri, sia per
i limiti di precisione dello strumento di misura sia per
gli errori dovuti al rilevatore. In altre parole il diametro
non può essere osservato con una precisione assoluta,
senza perdere alcuna cifra decimale. Tuttavia le v.c. continue
hanno un grande rilievo per la statistica come modelli approssimati
di situazioni reali. Di seguito si darà la definizione
della distribuzione di probabilità nel caso di v.c.
continue secondo un approccio intuitivo.
Supponiamo di avere
suddiviso l'intervallo in cui è definito il diametro
di un bullone in classi di uguale ampiezza, e di avere assegnato
a ciascuna di esse un livello di probabilità:
Tabella 1
| diametro
(mm.) |
probabilità |
| 140-150 |
0.05 |
| 150-160 |
0.09 |
| 160-170 |
0.20 |
| 170-180 |
0.32 |
| 180-190 |
0.20 |
| 190-200 |
0.09 |
| 200-210 |
0.05 |
| |
|
| totale |
1.00 |
Si ha così
una distribuzione di probabilità; il livello di probabilità
assegnato ad una certa classe indica la probabilità
di osservare, in una estrazione casuale dalla popolazione,
un diametro compreso nella classe.
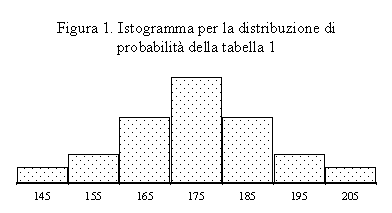
Tale distribuzione
può essere rappresentata graficamente mediante un
istogramma, in cui l'area di ciascun rettangolo è
pari alla probabilità della classe corrispondente
(figura 1)
Si supponga ora
di prendere classi di X sempre più piccole. Se ad
esempio consideriamo classi di ampiezza pari ad un quarto
di quelle precedenti, otterremo un nuovo istogramma dal
profilo più regolare, mentre resta invariato il significato
dell'altezza e dell'area di ogni singolo rettangolo dell'istogramma.
Sospingendo sempre più avanti il processo di riduzione
delle classi, si intuisce che la spezzata che delimita superiormente
l'istogramma, costituita da segmenti sempre più piccoli,
tende ad identificarsi con una curva continua.
Sia y = f(x) l'equazione
di questa curva. Il valore di f(x) corrispondente al generico
valore di X esprime, come altezza del singolo rettangolo
dell'istogramma, la densità di probabilità,
il prodotto f(x)x, rappresentato dal rettangolo tratteggiato
nella figura seguente, fornisce la probabilità che
X assuma un valore nell'intervallo di centro x e ampiezza
x.
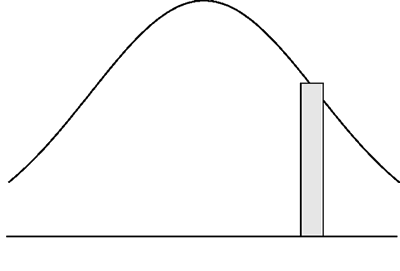
E' evidente che
una figura simile, detta funzione di densità,
è tale che l'area ad essa sottostante è pari
all'unità.
Più in generale
si definisce funzione di densità della variabile
casuale continua X, definita in un intervallo (l,L), la
funzione f(x) che possiede le seguenti proprietà:
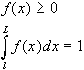
Inoltre si definisce
come funzione cumulativa di distribuzione o funzione di
ripartizione, sempre della variabile casuale continua X,
la:
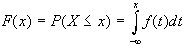
4.
Distribuzioni di probabilità congiunte
A volte si può
essere interessati all'esame congiunto di due variabili
casuali; ad esempio peso e spessore di un determinato prodotto,
numero di pezzi difettosi e numero di macchine utilizzate
per fabbricarli, ecc. E' quindi il caso di una analisi congiunta
di due variabili casuali.
Se X e Y sono due
v.c. che possono assumere rispettivamente valori (x1,x2
..... xn)
e (y1,y2.....yn)
e si è interessati all'evento congiunto in cui X
= xi
e Y = yi
, allora la v.c. congiunta è rappresentata dalla
coppia (xi
, yi)
alla quale corrisponde la probabilità P(X = xi
, Y = yi).
Le coppie ordinate del tipo (xi
,yi),
P(X = xi
, Y = yi)
descrivono la distribuzione congiunta di probabilità.
Se consideriamo
l'esempio del lancio della moneta per tre volte e definiamo
le v.c.:
X: 1 se il primo
lancio presenta Testa
0 altrimenti
Y: numero totale
di teste nei tre lanci
avremo:
spazio campione X Y probabilità
T T T 1 3 1/8
T T C 1 2 1/8
T C T 1 2 1/8
T C C 1 1 1/8
C T T 0 2 1/8
C T C 0 1 1/8
C C T 0 1 1/8
C C C 0 0 1/8
la distribuzione congiunta
sarà perciò data da:
| X
Y |
0 |
1 |
2 |
3 |
p(x) |
| 1 |
0 |
1/8 |
2/8 |
1/8 |
4/8 |
| 0 |
1/8 |
2/8 |
1/8 |
0 |
4/8 |
| p(y) |
1/8 |
3/8 |
3/8 |
1/8 |
1 |
La colonna indicata
con p(x) e la riga p(y) sono dette distribuzioni marginali
e rappresentano le distribuzioni delle singole variabili
senza prendere in considerazione la relazione con l'altra
variabile.
Utilizzando le probabilità
congiunte e quelle marginali è possibile determinare
le distribuzioni condizionate di probabilità; si
avrà quindi:
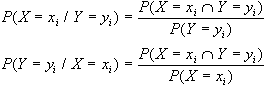
Distribuzione condizionata
di X dato Y
| X
Y |
0 |
1 |
2 |
3 |
| 1 |
0/(1/8)=0 |
(1/8)/(3/8)=1/3 |
(2/8)/(3/8)=2/3 |
(1/8)/(1/8)=1 |
| 0 |
(1/8)/(1/8)=1 |
(2/8)/(3/8)=2/3 |
(1/8)/(3/8)=1/3 |
0/(1/8)=0 |
| p(y) |
1 |
1 |
1 |
1 |
Distribuzione condizionata
di Y dato X
| X
Y |
0 |
1 |
2 |
3 |
p(x) |
| 1 |
0/(4/8)=0 |
(1/8)/(4/8)=1/4 |
(2/8)/(4/8)=1/2 |
(1/8)/(4/8)=1/4 |
1 |
| 0 |
(1/8)/(4/8)=1/4 |
(2/8)/(4/8)=1/2 |
(1/8)/(4/8)=1/4 |
0/(4/8)=0 |
1 |
Diremo che due variabili
casuali sono indipendenti se:
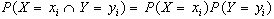
Partendo da questa condizione
è immediato dedurre che, affinchè due v.c.
siano indipendenti, deve risultare che, per ogni valore
di X
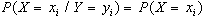
o per ogni valore di
Y
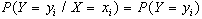
5.
Parametri delle distribuzioni di probabilità
Una distribuzione
di probabilità può essere rappresentata in
modi diversi (grafici, tabelle, funzioni), a volte però
può essere sufficiente una sintesi di tali distribuzioni.
Si possono cioè osservare solamente alcune caratteristiche
della distribuzione, sintetizzabili in uno o più
valori numerici in grado di fornire sufficienti informazioni
sulla distribuzione.
I due aspetti principali
di una distribuzione sono costituiti da misure di
tendenza centrale (i valori assunti in media dalla
v.c.) misure di dispersione o variabilità
(la tendenza dei valori della v.c. a differire tra loro).
5.1
Valore medio di una variabile casuale
Tra le misure di
tendenza centrale particolare importanza riveste la speranza
matematica o valore medio atteso indicato con
E(X):
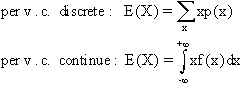
esempio: in una scommessa
un individuo ha probabilità di 2/5 di vincere 10
e probabilità 3/5 di perdere 5: il valore medio atteso
di questa distribuzione di probabilità sarà:
E(X)=10(2/5)+(-5)(3/5)=1
1 è la vincita
attesa se il giocatore ripete la scommessa un certo numero
di volte.
Le proprietà
del valore medio atteso sono:
1. se a è
una costante E(aX)=aE(X)
2. E(a+X)=a+E(X)
3. se a e b sono
costanti: E(aX+b)=aE(X)+b
4. data la v.c. X
e la sua E(X), la v.c. definita come scarto da E(X) ha valore
pari a 0:
E[X-E(X)]=0
E[X-E(X)]=E(X)-E[E(X)]=E(X)-E(X)=0
5. se X è
una v.c. con E(X) e Y è una v.c. con E(Y) allora:
E(X+Y)=E(X)+E(Y)
6. dato un numero
finito di v.c. il valore medio atteso della somma delle
v.c. è pari alla somma dei valori medi delle singole
v.c.:
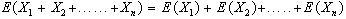
Evidentemente se
le n v.c. sono identiche tra loro si avrà:

Questa relazione
è particolarmente utile nel caso in cui si debba
calcolare la 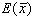 di una v.c.
di una v.c. 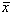 valore medio dei risultati di una estrazione con ripetizione.
Se n è la numerosità del campione, la v.c.
valore medio dei risultati di una estrazione con ripetizione.
Se n è la numerosità del campione, la v.c.
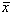 è
definita da:
è
definita da: 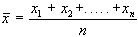
Quindi avremo che:
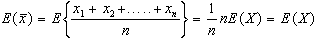
Questo significa
che le medie dei campioni estratti da una v.c. descrivono
una distribuzione che ha valore medio atteso pari al valore
medio atteso della v.c. oggetto del campionamento.
7. date due v.c.
X con E(X) e Y con E(Y), se X e Y sono indipendenti avremo
che
E(XY)=E(X)E(Y)
5.2
Misure di variabilità
Una prima misura della
variabilità può essere fornita dalla deviazione
del valore x dalla sua media: d=x-E(X). Si può quindi
costruire una media E[X-E(X)], ma il valore degli scarti
è sempre pari a 0. Si possono quindi utilizzare i
quadrati. Si otterrà quindi la varianza della v.c.
X:
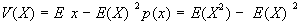
Per la Varianza di una
v.c. valgono le seguenti proprietà:
1. se a è
una costante V(a+X)=V(X)
2. V(aX)=a²V(X)
3. se a e b sono
costanti V(aX+b)=a²V(X)
5.3
Momenti delle distribuzioni congiunte
Nel caso di due v.c.
X e Y, assume particolare importanza il valore medio atteso
del loro prodotto. Essendo E(XY)=E(X)E(Y) nel caso in cui
le due v.c. siano indipendenti, il loro prodotto può
essere utilizzato per misurare la forza della relazione
che le lega.
Una misura caratterizzante
la distribuzione congiunta di X e Y, che esprime la direzione
della relazione tra le due v.c. è la covarianza:
COV(XY)=E[(X-E(X)(Y-E(Y))]
=E[XY-YE(X)-XE(Y)+E(X)E(Y)]
=E(XY)-E(X)E(Y)-E(Y)E(X)+E(X)E(Y)
=E(XY)-E(X)E(Y)
Dal punto di vista calcolatorio
la covarianza si ottiene, nel caso di v.c. discrete come:
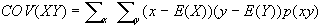
Evidentemente se X e
Y sono indipendenti, avremo che E(XY)-E(X)E(Y)=0 e quindi
E(XY)=E(X)E(Y), per cui si avrà COV(XY)=0.
E' da notare che nell'effettuare
il prodotto tra gli scarti di X e di Y avremo che se ad
alti (bassi) valori di X corrispondono alti (bassi) valori
di Y si ha un legame positivo tra le due v.c., espresso
da valori positivi della covarianza. Se invece sussiste
una relazione inversa tra le due v.c. (ad alti valori di
X corrispondono bassi valori di Y o viceversa) il prodotto
degli scarti condurrà a valori negativi della covarianza.
La covarianza risulta
espressa in termini dell'unità di misura di X e Y.
E' possibile esprimere la relazione tra X e Y in termini
di puri numeri tramite il coefficiente di correlazione
:
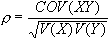
Il coefficiente di correlazione
assume valori compresi tra -1 e 1. Quando =1 le variabili
risultano perfettamente correlate in senso positivo, mentre
se è pari a -1 lo saranno in senso negativo. Se invece
=0, vorrà dire che COV(XY)=0, quindi non esiste relazione
tra le due v.c..
Riprendendo le proprietà
della varianza di due v.c. avremo che:
V(X+Y)=V(X)+V(Y)+2COV(XY)
V(X-Y)=V(X)+(VY)-2COV(XY)
esempio:
| Y
X |
0 |
1 |
2 |
3 |
p(y) |
| 1 |
1/8 |
0 |
0 |
1/8 |
2/8 |
| 2 |
0 |
1/8 |
1/8 |
0 |
2/8 |
| 3 |
0 |
2/8 |
2/8 |
0 |
4/8 |
| p(x) |
1/8 |
3/8 |
3/8 |
1/8 |
1 |
E(X)=0(1/8)+1(3/8)+2(3/8)+3(1/8)=12/8=3/2
E(Y)=1(2/8)+2(2/8)+3(4/8)=18/8=9/4
E(XY)=(0)(1)(1/8)+(3)(1)(1/8)+(2)(1)(1/8)+(2)(2)(1/8)+(3)(1)(2/8)+(3)(2)(2/8)=27/8
E(X²)=0²(1/8)+1²(3/8)+2²(3/8)+3²(1/8)=24/8=3
E(Y²)=1²(2/8)+2²(2/8)+3²(4/8)=42/8=21/4
V(X)=E(X²)-[E(X)]²=3-(3/2)²=3/4
V(Y)=E(Y²)-[E(Y)]²=(21/4)-(9/4)²=3/16
COV(XY)=E(XY)-E(X)E(Y)=(27/8)-[(3/2)(9/4)]=(27/8)-(27/8)=0
evidentemente il coefficiente
di correlazione sarà pari a 0.
MODELLI
DISTRIBUTIVI
Uno dei principali compiti
di un ricercatore consiste nell'individuazione di una legge
che meglio permetta di descrivere il fenomeno che sta indagando.
Quando il fenomeno implica situazioni di incertezza (che
portano quindi ad escludere modellizzazioni di tipo deterministico)
ci si deve ricondurre alla elaborazione di modelli probabilistici
che consentano di interpretare le informazioni disponibili.
La nozione di modello
si riferisce generalmente ad una espressione matematica
che in qualche modo riguarda la possibilità del verificarsi
dei risultati di una astratta situazione sperimentale.
Quando l'analisi della
situazione reale permette di ricondurre il complesso delle
informazioni raccolte ad uno schema interpretativo, corrispondente
alle assunzioni che caratterizzano il modello astratto,
è possibile per il ricercatore adottare il modello
come strumento deduttivo.
I modelli probabilistici
sono di notevole interesse pratico perchè propongono
una precisa formulazione matematica di molte situazioni
che si incontrano frequentemente nella realtà sperimentale.
In molte situazioni reali, diverse tra loro, è possibile
adottare lo stesso modello interpretativo, solo i parametri
di tale modello varieranno in funzione del problema specifico.
Le variabili casuali
che emergono, interpretando distinte situazioni reali, vengono
così ad essere descritte da distribuzioni di probabilità
che possono essere studiate e algebricamente manipolate,
indipendentemente dalle loro specifiche applicazioni.
La scelta del modello
della distribuzione di probabilità da adattare ad
un particolare problema, molto spesso, è condotta
per mezzo del confronto tra la forma dell'istogramma dei
dati osservati e la forma della funzione di densità
(FDP) o funzione di ripartizione (FMP) di una particolare
distribuzione nota. A volte questo esame può essere
l'unico approccio al problema, ma è da sottolineare
che le conclusioni a cui si arriverà saranno tanto
più errate tanto più le assunzioni del modello
di base sono lontane dal descrivere e interpretare la situazione
reale. E' quindi auspicabile che la scelta del modello si
basi principalmente sulla comprensione del fenomeno.
1. Modelli
distributivi discreti
1.1 Modello
di Bernoulli
E' il più semplice
dei modelli probabilistici, e si riferisce ad una situazione
sperimentale in cui si hanno due soli risultati: l'evento
E e il suo opposto 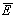 .
.
Si ha quindi a che fare
con una v.c. che può assumere solo 2 valori: E con
probabilità p e 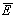 con probabilità (1-p):
con probabilità (1-p):
si può quindi
esprimere la funzione di massa di probabilità (FMP)
come:
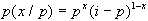
In questo caso avremo:
E(X)=0(1-p)+1p=p
E(X²)=0²(1-p)+1²p=p
V(X)=p-p²=p(1-p)
1.2 Modello
Binomiale
Se abbiamo una situazione
sperimentale in cui:
1. numero n di prove
indipendenti tra loro
2. ciascuna prova
è di tipo bernoulliana E,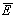
3. in tutte le prove
la probabilità p, dell'evento E, si mantiene costante,
e quindi anche la probabilità di 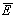 è sempre (1-p)
è sempre (1-p)
e se in tale situazione
si è interessati al numero di eventi E risultanti
nel ripetersi delle prove, si può derivare una v.c.
X, detta binomiale, che rappresenta il numero X degli
eventi E che si manifestano nelle n prove.
Ad esempio una v.c.
binomiale è data dal numero di teste che si presentano
lanciando una moneta per tre volte; al numero di pezzi difettosi
che si possono avere osservando 20 pezzi prodotti da una
macchina.
La probabilità
che su n prove si verifichi x volte l'evento E, sarà
data da 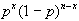 .
Questa probabilità deve essere moltiplicata per il
numero di possibili sequenze in cui si hanno x eventi E
e n-x eventi
.
Questa probabilità deve essere moltiplicata per il
numero di possibili sequenze in cui si hanno x eventi E
e n-x eventi 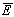 .
Il numero di queste possibili sequenze è dato dalla
combinazione di x eventi E e n-x eventi
.
Il numero di queste possibili sequenze è dato dalla
combinazione di x eventi E e n-x eventi 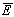 ,
cioè:
,
cioè:
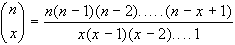
Ad esempio, la probabilità
di avere 3 pezzi non difettosi su 4 osservati sarà
data da:
ND ND ND D
ND ND D ND ognuna
di queste sequenze avrà prob.=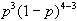
ND D ND ND
D ND ND ND
dove la probabilità
di non difettoso (ND) è sempre p, mentre quella di
difettoso (D) è (1-p); inoltre il numero di sequenze
possibili, in cui si possono avere 3 ND e 1 D sarà:
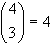
quindi la probabilità
di avere 3 non difettosi su 4 sarà:
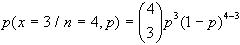
supponendo di avere
precedentemente verificato che la probabilità di
un pezzo non difettoso nella produzione in esame sia pari
a 0.95, avremo che la probabilità in oggetto sarà:
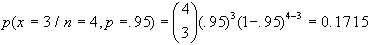
In generale la funzione
di massa di probabilità (FMP) della distribuzione
binomiale è data da:
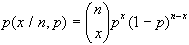
La funzione di ripartizione
(FCD) è invece data da:
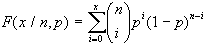
che esprime la probabilità
di una v.c. di tipo binomiale di assumere valori inferiori
ad un certo x.
Il valore medio atteso
sarà: E(X)=np, infatti ogni v.c. X, numero di successi
su n prove, può essere considerata come somma di
n v.c. identiche tra loro di tipo bernoulliano, ognuna con
valore medio p; quindi  =np.
=np.
La varianza di una v.c.
binomiale sarà V(X)=np(1-p).
Esempio: se il 20% dei
bulloni prodotti da una macchina è difettoso, determinare
la probabilità che su 4 bulloni scelti a caso ve
ne siano a) 1 difettoso, b) nessun difettoso, c) al massimo
3 difettosi.
a) p=0.20 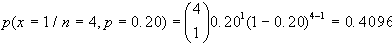
lo stesso risultato
lo si può ottenere consultando la tavola IIIb nella
pagina seguente. In essa, per diversi valori di n, x,
p, sono riportate le probabilità binomiali.
b) p=0.20 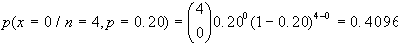
c) 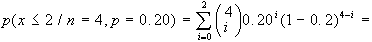
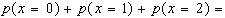
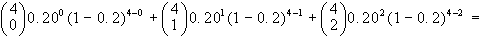
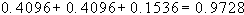
1.3 Modello
ipergeometrico
Utile nel rappresentare
situazioni tipiche del controllo di accettazione. Si differenzia
dal modello binomiale per le condizioni di costanza del
valore di probabilità degli eventi da prova a prova
e dell'indipendenza delle prove.
In questo caso si ipotizza
una popolazione composta da N elementi K dei quali hanno
una certa caratteristica, ed, evidentemente N-K non la posseggono.
Selezionando un elemento
di questi N, potremo osservare uno dei K (successo) o uno
degli N-K. Ripetendo le prove n volte senza ripetizione,
senza cioè reimmettere gli elemeti estratti, ciascuna
prova è condizionata dai risultati precedenti e la
probabilità di successo o insuccesso si modifica
da prova a prova.
Sarà quindi possibile
determinare quale sia la probabilità di avere in
n prove x elementi dei K di un tipo e n-x elementi degli
N-K.
Il numero complessivo
dei casi possibili sarà dato dal numero di possibili
modi in cui possono essere scelti gli n tra gli N dati:
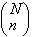 .
.
Inoltre gli x elementi
dei K possono presentarsi in 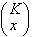 modi diversi, mentre gli n-x dell'altro tipo possono presentarsi
in
modi diversi, mentre gli n-x dell'altro tipo possono presentarsi
in 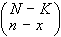 modi diversi. Quindi:
modi diversi. Quindi:
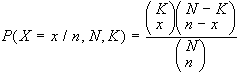
Il valore medio atteso
E(X) di questa distribuzione è data da: 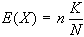 mentre la varianza è:
mentre la varianza è: 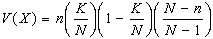 .
.
Esempio 1: se vengono
estratte 4 carte da un mazzo da poker contenente i soli
onori (A,K,Q,J,10), con quale probabilità si avranno
a) 1 asso, b) 4 assi:
a) N=20, K=4, n=4, x=1
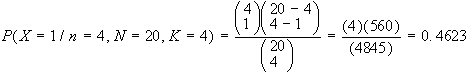
b) N=20, K=4, n=4, x=0
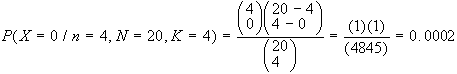
Esempio 2: in un lotto
di 15 lampadine ve ne sono 4 difettose. Se si estrae, per
decidere l'accettazione dell'intero lotto, un campione di
3 elementi, con quale probabilità si avranno nel
campione a) nessun difettoso, b) 2 difettosi , c) 3 difettosi?
a) N=15, K=4, n=3, x=0
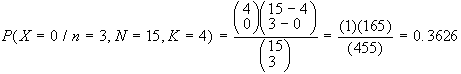
b) N=15, K=4, n=3, x=3
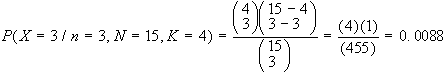
1.4 Modello
di Poisson
Si riprenda la distribuzione
binomiale e si ponga np=, dove è una costante positiva,
rappresentando il valore medio atteso di tale distribuzione.
Poichè p=/n si può scrivere:
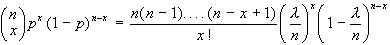
Quindi:
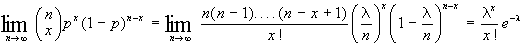
In termini imprecisi
si può dire che, se n, in modo che np=, la distribuzione
binomiale tende ad una forma limite che va sotto il nome
di distribuzione di Poisson, la cui funzione di massa di
probabilità è data da:
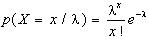
In termini più
descrittivi si può fare riferimento ad una situazione
sperimentale in cui non si è in grado di definire
preventivamente una sequenza finita di prove, come nel caso
della binomiale, perchè gli eventi si manifestano
in una dimensione continua, come ad esempio il tempo o lo
spazio.
Un esempio può
essere rappresentato dall'arrivo di una macchina ad un incrocio,
oppure dal presentarsi di un pezzo difettoso al punto di
controllo, in un intervallo di tempo t. Data una situazione
sperimentale di questo tipo si può ricondurla ad
una situazione simile a quella della binomiale considerando
n intervalli del tempo t, tutti di uguale ampiezza t/n,
e considerare t come composto da n prove indipendenti, caratterizzate
ognuna da una v.c. di tipo bernoulliano "arrivo", "non arrivo".
Per rendere però impossibile il verificarsi di due
eventi in un intervallo t/n si dovrà aumentare il
numero di intervalli n, riducendo quindi la loro ampizza
t/n. Se consideriamo il valore medio atteso degli eventi
nel periodo t, secondo lo schema binomiale, si deve avere
che E(X)=np. Quindi, al crescere di n (numero di intervalli
e quindi numero di prove), l'ampiezza degli intervalli (t/n)
diverrà sempre più piccola, riducendosi quindi
anche la probabilità p che si manifesti un evento
in ogni singola prova.
Secondo questa impostazione
anche situazioni con eventi che si manifestano in una dimensione
continua, non immediatamante riconducibile alle sequenze
di prove, possono essere considerate rappresentabili da
un modello binomiale con il numero di prove tendente ad
infinito e valore medio atteso costante.
La funzione di ripartizione
(FCD) del modello di Poisson è data da:
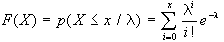
I valori della funzione
di ripartizione della Poisson sono riportati nella Tav.
A-6 nella pagina seguente.
Esempio: una macchina
produce in media 3 pezzi difettosi ogni ora; determinare
la probabilità che la macchina produca in 1 ora:
a) 3 pezzi difettosi, b) nessun pezzo difettoso, c) non
più di 3 difettosi, d) 3 o più pezzi difettosi,
e) 7 difettosi in 2 ore.
a) 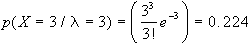
utilizzando la tavola
si debbono invece considerare le due probabilità
cumulate p(X3) e p(X2), e per differenza calcolare quella
di p(X=3), infatti p(X3) rappresenta la probabilità
di avere 0,1,2,3 difettosi, mentre p(X2) fornisce la probabilità
di avere 0,1,2 difettosi; quindi:
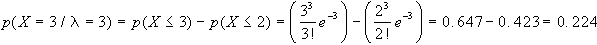
b) 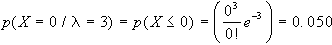
c) 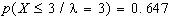
d) 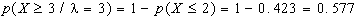
e) 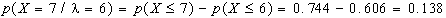
Esempio 2: un produttore
di transistor garantisce una vita utili maggiore di 2000
ore, una precedente esperienza assicura che 4 transistor
su 100 si guastano entro le 2000 ore. Determinare quale
sia a) la probabilità di non avere alcun guasto entro
le prime 2000 ore, b) la probabilità di uno o più
guasti entro le 2000 ore.
a) =4/100=0.04 (guasti/2000
ore) p(X=0/=0.04)=0.961
b) =0.04 p(X1/=0.04)=1-p(X=0/=0.04)=1-0.961=0.039
2. Modelli
distributivi continui
Se X è una variabile
casuale che può assumere qualsiasi valore in un insieme
non numerabile allora si dice di tipo continuo. Se è
possibile suddividere l'insieme infinito in cui è
definita X in un insieme numerabile di intervalli distinti
ed esiste una funzione f(x) (funzione di densità
di probabilità FDP) tale che:
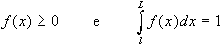
allora è definibile
come probabilità dell'intervallo tra due valori a
e b di X (con ba) la funzione:
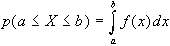
E' inoltre possibile
definire la funzione di ripartizione o funzione cumulativa
di distribuzione (FCD) come:
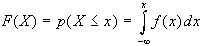
Particolarmente interessante
è il caso in cui la v.c. contiuna è rappresentata
dal tempo. In questo caso acquisiscono particolare interesse
alcune funzioni utilizzate nella valutazione dell'affidabilità
di un processo o della durata nel tempo.
Definiamo affidabilità
la probabilità che un sistema o unità mantenga
le sue prefissate condizioni di funzionamento sotto certe
condizioni ambientali per un tempo prefissato. In altri
termini si tratta di una misura della probabilità
che ha il sistema di non guastarsi e quindi di funzionare
in un definito intervallo di tempo. Quindi se t è
la v.c. continua tempo e T la variabile tempo del guasto,
f(t)dt la FDP di guasto, cioè una misura della probabilità
di guasto nell'intervallo t-t+dt. Allora la funzione di
affidabilità del sistema al tempo t, siboleggiata
con R(t), è data da:
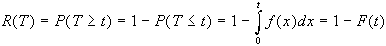
Si noti che la funzione
di affidabilità R(t) è il complemento all'unità
della funzione di ripartizione ed esprime la probabilità
che del sistema di non guastarsi prima dell'istante t.
Altra funzione, rilevante
negli studi di affidabilità, è il cosiddetto
tasso di guasto indicato con (t), definibile come
la probabilità che il sistema si guasti al tempo
T, quando non si sia guastato prima di T. Si ha, dalla definizione:
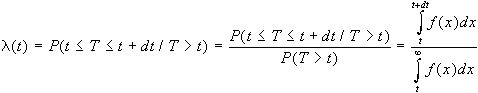
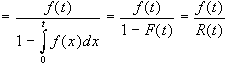
2.1 Modello
normale o gaussiano
Una v.c. si distribuisce
normalmente, cioè secondo un modello normale o gaussiano,
quando la sua funzione di densità di probabilità
è:
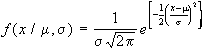
In generale questo tipo
di distribuzione è ipotizzabile per un certo fenomenoquando
le sue misure sono composte da una parte da un sistema di
cause costante, dall'altra da un errore giustificato da
un insieme di cause contrastanti e indipendenti tra loro.
La normale è
completamente descritta dai parametri e ², infatti l'esponente
è l'unica parte variabile. In realtà si tratta
quindi di una famiglia di distribuzioni, ognuna caratterizzata
da una coppia (, ²). Le distribuzioni normali possono quindi
differire per media o per varianza o per entrambi. La media
rappresenta un parametro di locazione e determina lo spostamento
sull'asse X, mentre ² determina la forma della curva.
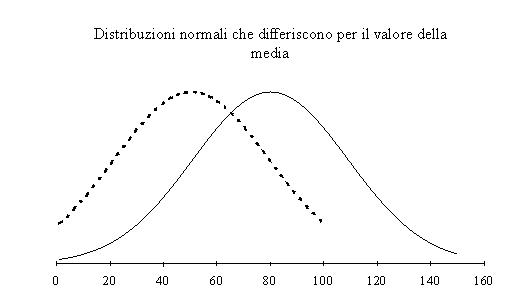
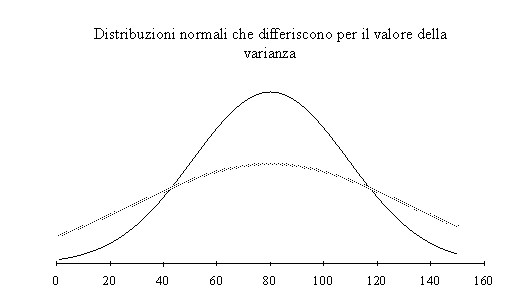
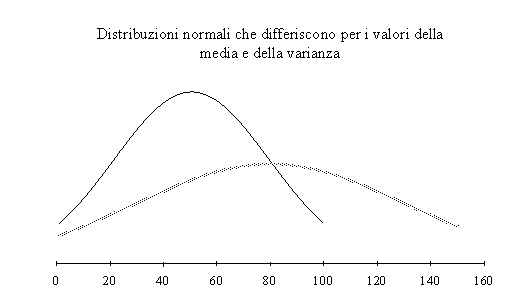
Si deve inoltre sottolineare
che la distribuzione normale presenta la caratteristica
che per intervalli simmetrici rispetto alla media e funzione
dello scarto quadratico medio, l'area sottostante alla curva
è sempre rappresentata da una particolare percentuale
del totale dell'area (che essendo una probabilità
è pari ad 1).
In particolare se consideriamo
l'intervallo - |--| + l'area sottea alla curva in tale intervallo
è sempre pari al 68% dell'area totale; se invece
consideriamo l'intervallo -1.96 |--| +1.96 l'area sarà
pari al 95% dell'area complessiva.
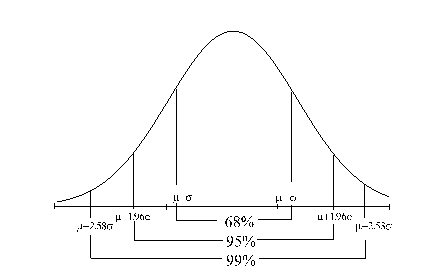
La funzione di ripartizione
(FCD) della distribuzione normale è data da:
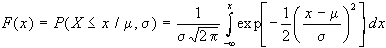
Il valore medio atteso
di una distribuzione normale è E(X)=, mentre la varianza
è V(X)=².
Evidentemente, per calcolare
la probabilità che una v.c. distribuita secondo una
normale assuma un valore inferiore ad un certo valore x
di X o interno ad un certo intervallo, si dovrà calcolare
l'integrale presentato nella funzione di ripartizione, essendo
ogni distribuzione normale caratterizzata da un suo valore
medio e da una sua varianza. Per evitare questo inconveniente
si può procedere ad una trasformazione della variabile,
in modo tale da ricondurre tutte le possibili v.c. di tipo
normale ad un unica distribuzione normale con media pari
a 0 e varianza uguale ad 1. Si tratta in altri termini di
trasformare una distribuzione normale con media e varianza
² in una variabile standardizzata z, calcolata come
segue:
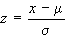
la quale è ancora
distribuita normalmente, ma con =0 e ²=1. Si potrà
quindi trasformare qualunque distribuzione normale con e
² dati in una v.c. normale standardizzata, per la quale
sono stati tabulati i valori della funzione di ripartizione
(Tavola IV nella pagina seguente).
Esempio 1: determinare
la probabilità che: a) z2, b) z1.45
a) P(z2.00)=0.5+0.4772=0.9772
la tavola IV riporta
il valore della probabilità dell'intervallo compreso
tra la media 0 ed il valore di z (in questo caso pari a
2.00); per ottenere quindi la probabilità che z sia
minore di 2 si dovrà sommare al valore di probabilità
desunto dalla tavola il valore di 0.5 che rappresenta la
probabilità di avere un valore inferiore a 0:
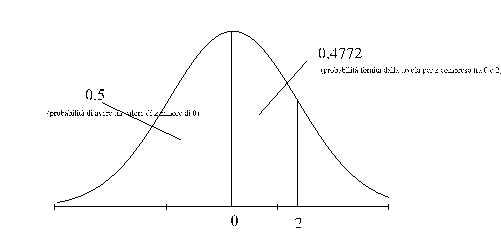
b) P(z1.45)=0.5+0.4265=0.9265
Esempio 2: data una
v.c. X distribuita normalmente con media=50 e s.q.m.=5 determinare
la probabilità che: a) X sia minore di 57.5, b) X
sia compreso tra 49 e 52:
a) prima di tutto si
deve calcolare z: 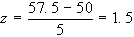
avremo quindi P(z1.5)=0.5+0.4332=0.9332
b) in questo caso avremo
due valori di z: 
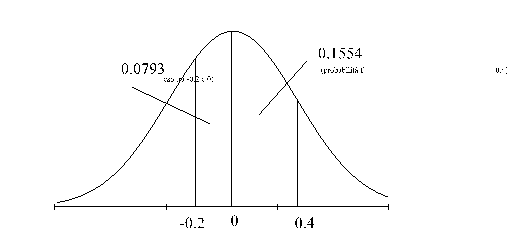
quindi P(-0.2z0.4)=P(-0.2z0)+P(0z0.4)=0.0793+0.1554=0.2347
Se abbiamo n v.c. 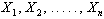 distribuite tutte normalmente, la v.c. somma di queste n
v.c.
distribuite tutte normalmente, la v.c. somma di queste n
v.c. 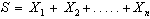 sarà ancora distribuita normalmente:
sarà ancora distribuita normalmente:
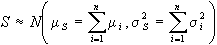
Esempio: nell'assemblaggio
di un prodotto intervengono 4 componenti, prodotti indipendentemente
uno dall'altro. La lunghezza del prodotto assemblato è
data dalla somma delle lunghezze dei 4 componenti. La lunghezza
del prodotto assemblato è una v.c. che indichiamo
con Y, mentre le lunghezze dei 4 componeneti sono 4 v.c.
distribuite normalmente con:
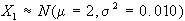
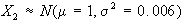
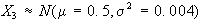
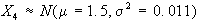
Se le specifiche del
prodotto assemblato sono 5-0.10Y5+0.10, determinare con
quale probabilità la produzione di Y sarà
accettabile come non difettosa.
Siccome la media di
Y è pari alla somma delle medie delle sue componenti
avremo che:
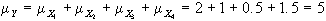
mentre lo scarto quadratico
medion sarà:
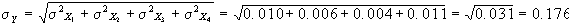
per cui dovremo calcolare:
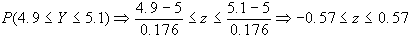
questo fornirà
una probabilità pari a:
P(4.9Y5.1)=0.2157+0.2157=0.4314
Potremo quindi anche
dire che il 43% della produzione del prodotto assemblato
sarà conforme alle specifiche fornite.
La distribuzione normale
rappresenta inoltre una approssimazione di altre distribuzioni,
in quanto costituisce una forma limite alla quale tendono
molte altre distribuzioni (ipergeometrica, poisson, binomiale,
ecc.).
Nel caso di un esperimento
di tipo binomiale in cui il numero di prove è molto
elevato, diviene difficoltoso calcolare la probabilità
di un valore di X. Però, con n, la distribuzione
binomiale tende ad una distribuzione normale con =np e con
²=np(1-p). Sarà quindi possibile calcolare:
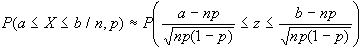
Esempio: determinare
la probabilità di osservare un numero di pezzi difettosi
compreso tra 29 e 46, avendo estratto dall'intera produzione
di una macchina un campione di 100 unità e sapendo
che la macchina produce con un tasso di difettosità
pari al 40%.
in questo caso avremo
p=0.40, per cui:
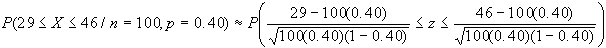
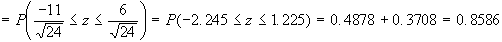
CAMPIONAMENTO
E DISTRIBUZIONI CAMPIONARIE
In questo capitolo,
prendendo le mosse dalle nozioni di popolazione e campione
e da quelle di distribuzione del campione, si perverrà
alla definizione dell'inferenza statistica nelle sue diverse
articolazioni. Verranno inoltre illustrate le distribuzioni
campionarie di alcune particolari funzioni dei dati del
campione (statistiche), distribuzioni che sono la premessa
indispensabile per poterevrisolvere i problemi concreti
di inferenza.
1. Popolazione
e campione
Come è noto,
l'indagine statistica verte sempre su insiemi di unità
in cui si manifesta il fenomeno che si studia. Questi insiemi
vanno sotto il nome di popolazioni o collettivi
statistici o universo di riferimento, e possono
essere costituiti da un numero finito o infinito di unità;
nel primo caso si parla di popolazioni finite, nel
secondo di popolazioni infinite.
La conoscenza delle
caratteristiche di una popolazione finita può essere
conseguita osservando la totalità delle unità
della popolazione, oppure un sottoinsieme di queste, un
campione. Una popolazione infinita, invece, può
essere studiata solo tramite un campione. Per chiarire questi
concetti può risultare opportuno fare un esempio.
Si supponga di volere
studiare la distribuzione del diametro delle rondelle contenute
in lotto di prodotto (ad esempio di 1000 pezzi). In questo
caso l'osservazione di tutti i pezzi del lotto può
risultare troppo oneroso, si può quindi procedere
all'esame di una parte del lotto. In questo esempio l'insieme
di rondelle appartenenti al lotto costituisce una popolazione
finita.
Se invece consideriamo
la produzione di una macchina che produce rondelle e vogliamo
studiare il diametro dei pezzi prodotti da tale macchina,
osserveremo una parte di tale produzione la quale rappresenterà
un campione della produzione. Tuttavia, rispetto all'esempio
precedente, a fronte del campione osservato, non esiste
una popolazione ben definita, una totalità di elementi
di cui quelli osservati sono una parte. In altri termini
si può dire che un insieme di pezzi prodotti e osservati
per allo scopo del controllo del processo costituisce un
campione dei pezzi che la macchina può produrre nelle
stesse condizioni. Questo insieme potenziale è una
popolazione infinita.
2. Il
campione casuale
Data una popolazione
finita di N unità, si consideri l'operazione consistente
nell'estrarre a sorte un'unità, nell'osservarvi il
valore di una certa caratteristica quantitativa X, e nel
riporla nella popolazione. Si ammetta che l'operazione sia
effettuata in modo che ogni unità della popolazione
abbia la stessa probabilità di essere estratta, probabilità
pari ad 1/N. Si immagini di ripetere l'operazione n volte.
L'insieme delle unità così estratte costituisce
un campione casuale.
L'estrazione di un campione
può essere schematizzata mediante un'urna, dove ciascuna
unità della popolazione è rappresentata da
una pallina recante il valore che la caratteristica X assume
nell'unità. Da questo punto di vista, l'operazione
di estrazione consiste nella scelta a caso di una pallina,
nella registrazione del valore in essa indicato e nel riporre
la pallina nell'urna. Questo procedimento è denominato
campionamento con ripetizione.
Una variante a queso
procedimento si ha quando la singola estrazione nonè
seguita dal reinserimento della pallina nell'urna; in questo
caso si parla di campionamento senza ripetizione.
E' chiaro che nel campionamento
senza ripetizione le successive estrazioni non avvengono
in condizioni uniformi; infatti, da una estrazione all'altra
la popolazione si modifica. Tuttavia quando la dimensione
N della popolazione è molto elevata e l'ampiezza,
n, del campione è una frazione modesta di N, i due
tipi di campionamento sono praticamente equivalenti.
L'obiettivo che ci si
propone con il campionamento è quello di formare
un campione il più possibile rappresentativo
della popolazione, in modo che risultino accurate le informazioni
sulle caratteristiche della popolazione che si traggono
dal campione.
In generale si può
ritenere che quando si estrae un campione di n unità,
il risultato campionario può essere pensato come
l'espressione di n v.c. identiche tra loro 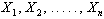 che possiedono cioè la stessa distribuzione della
popolazione di provenienza. Se ad esmpio consideriamo una
popolazione composta da un'urna in cui vi sono 2 palline
segnate con 1, 2 palline segnate con 3 e 4 palline segnate
con 5 e se estraiamo una pallina, il risultato campionario
"numero segnato sulla pallina" ha ovviamente la stessa distribuzione
di probabilità della popolazione di provenienza:
che possiedono cioè la stessa distribuzione della
popolazione di provenienza. Se ad esmpio consideriamo una
popolazione composta da un'urna in cui vi sono 2 palline
segnate con 1, 2 palline segnate con 3 e 4 palline segnate
con 5 e se estraiamo una pallina, il risultato campionario
"numero segnato sulla pallina" ha ovviamente la stessa distribuzione
di probabilità della popolazione di provenienza:
| X:
valore della pallina |
probabilità |
| 1 |
0.25 |
| 3 |
0.25 |
| 5 |
0.50 |
Considerare le osservazioni
campionarie come v.c. permette di ritenere che qualsiasi
quantità calcolata sui risultati del campione è
anch'essa una variabile casuale.
Il parametro campionario
ottenuto come funzione dei risultati campionari avrà
quindi una sua distribuzione di probabilità della
distribuzione parametrica campionaria o distribuzione
campionaria che può essere messa in relazione
con la distribuzione della popolazione.
Riprendendo l'esempio
dell'urna, costruiamo tutti i possibili campioni di numerosità
2 (n=2):
| X1,X2
|
probabilità |
| 1,1 |
(0.25)(0.25)=0.0625 |
| 1,3 |
(0.25)(0.25)=0.0625 |
| 1,5 |
(0.25)(0.50)=0.1250 |
| 3,1 |
(0.25)(0.25)=0.0625 |
| 3,3 |
(0.25)(0.25)=0.0625 |
| 3,5 |
(0.25)(0.50)=0.1250 |
| 5,1 |
(0.50)(0.25)=0.1250 |
| 5,3 |
(0.50)(0.25)=0.1250 |
| 5,5 |
(0.50)(0.50)=0.2500 |
| totale |
1 |
Se consideriamo la funzione
somma dei risultati campionari X1+X2
avremo che:
| X1+X2
|
probabilità |
| 2 |
1(0.0625)=0.0625 |
| 4 |
2(0.0625)=0.1250 |
| 6 |
2(0.1250)+0.0625=0.3125 |
| 8 |
2(0.1250)=0.2500 |
| 10 |
1(0.2500)=0.2500 |
| totale |
1 |
Questa è la distribuzione
campionaria del parametro campionario somma, per campioni
di numerosità n=2 estratti con ripetizione da una
popolazione data.
Riassumendo: dalla distribuzione
di una popolazione deriva la distribuzione dei possibili
valori di un parametro campionario, calcolato su ciascun
campione di numerosità n estratto secondo un preciso
schema campionario:
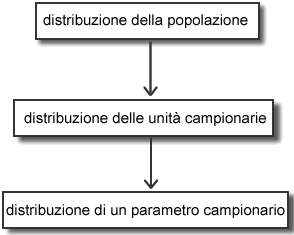
Avremo quindi distribuzioni
diverse a seconda del parametro campionario e a seconda
della numerosità del campione.
Come per ogni altra
distribuzione di probabilità è possibile,
anche per le distribuzioni campionarie, determinare il valore
medio atteso e la varianza per qualunque parametro :
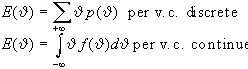
che esprime la tendenza
centrale, e quindi il valore attorno al quale tendono ad
assestarsi i valori calcolati su tutti i possibili campioni
del parametro .
V()=E[-E()]=E(²)-[E()]²
che esprime la misura
di dispersione dei possibili valori campionari di attorno
a E().
Nell'esempio precedente
dell'urna è facile determinare la distribuzione del
parametro campionario (nell'esempio la somma) e quindi calcolare
E() e V(); nella pratica però si ha a che fare con
situazioni più complesse, nelle quali è in
pratica difficile costruire la distribuzione campionaria
e di conseguenza calcolarne la madia e la varianza.
Per superare questo
problema è utile il teorema del limite centrale:
se 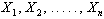 sono n variabili casuali indipendenti e identicamente distribuite,
ognuna con media
sono n variabili casuali indipendenti e identicamente distribuite,
ognuna con media 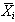 e varianza
e varianza 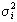 la variabile
la variabile 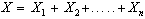 tende asintoticamente a distribuirsi secondo una normale
qualunque sia la distribuzione delle v.c.
tende asintoticamente a distribuirsi secondo una normale
qualunque sia la distribuzione delle v.c.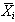 inoltre:
inoltre:
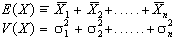
L'importanza di questo
teorema sta nel fatto che molti parametri campionari sono
esprimibili come funzioni della somma degli n risultati
campionari.
3. Distribuzione
campionaria delle medie
In base al teorema del
limite centrale si può ritenere che il valore medio
campionario 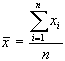
calcolato in un campione
scelto casualmente da una popolazione caratterizzata da
una media e da uno scarto quadratico medio , descrive, al
ripetersi del campionamento una distribuzione con valore
medio atteso 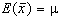 e varianza
e varianza 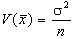 ;
inoltre se il campione è sufficientemente grande,
la distribuzione delle medie campionarie si approssima ad
una normale.
;
inoltre se il campione è sufficientemente grande,
la distribuzione delle medie campionarie si approssima ad
una normale.
Per quanto riguarda
la media campionaria abbiamo infatti che:
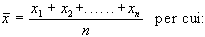
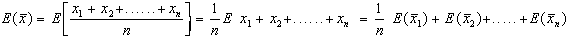
considerando ogni risultato
campionario come manifestazione di una stessa v.c., quindi
tutti con media e varianza uguali a quelli della popolazione
di provenienza, avremo:
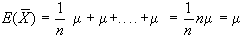
Analogamente per la
varianza V(X) avremo che:
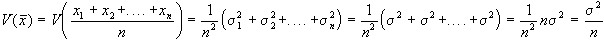
Quanto visto fino ad
ora vale per il caso in cui il campione si estratto con
ripetizione da popolazioni finite o da popolazioni infinite.
Nel caso in cui il campionamento
venga effettuato senza ripetizione da popolazioni finite
si dovrà tenere conto di un fattore di correzione.
In questo caso avremo che:
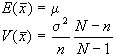
Esempio: 200 bulloni
hanno un diametro medio =8 cm con scarto quadratico medio
=0.2. Determinare la probabilità che un campione
estratto casualmente a) con ripetizione, b) senza ripetizione,
abbia un diamtero medio 1) minore di 7.5 cm, 2) minore di
8.1 cm, 3) compreso tra 7.95 e 8.08 cm.
a.1) si deve calcolare
il valore di z corrispondente a 7.5, tenendo conto che la
media è pari ad 8 e lo s.q.m. della distribuzione
della media campionaria è data dalla radice del rapporto
tra la varianza e la numerosità del campione; per
cui:
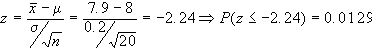
a.2) 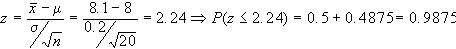
a.3) 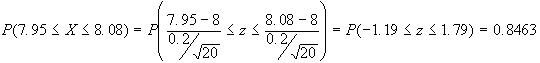
b.1) in questo caso
si modifica la varianza della distribuzione di riferimento,
avremo quindi:
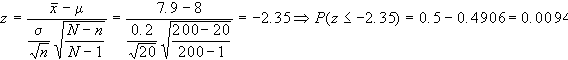
b.2) 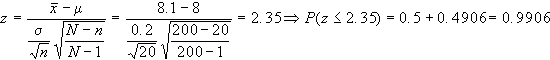
b.3)
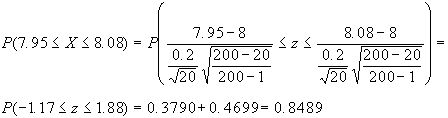
4. Distribuzione
campionaria del numero di successi e della proporzione
Partendo da una popolazione
di tipo bernoulliano, quindi caratterizzata da due soli
tipi di evento, successo (E) e insuccesso (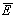 ),
consideriamo l'esempio Difettoso (1), NonDifettoso (0),
rispettivamente successo e insuccesso; avremo che:
),
consideriamo l'esempio Difettoso (1), NonDifettoso (0),
rispettivamente successo e insuccesso; avremo che:
per cui avremo che =
e ²= [(1-)].
Estraendo un campione
di numerosità n da una popolazione di questo tipo,
dove abbiamo indicato con 1 i difettosi e con 0 i non difettosi,
otterremo:
| 1 |
1 |
0 |
1 |
0 |
...... |
| D |
D |
ND |
D |
ND |
...... |
Quindi la somma campionaria
è uguale alla somma del numero di difettosi (successi),
perciò, siccome: 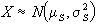 avremo che
avremo che 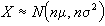 da cui otterremo che:
da cui otterremo che:
E(X)=n

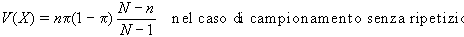
Sulla base di questi
parametri della distribuzione campionaria avremo che la
funzione di distribuzione del parametro campionario numero
di successi può essere scritta:

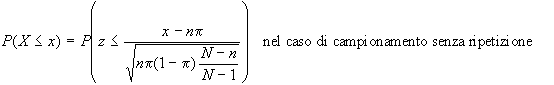
dove z è sempre
la distribuzione normale standardizzata.
Disorso molto simile
può essere fatto per determinare la distribuzione
della proporzione campionaria che indichiamo con 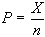 dove X rappresenta il numero di successi ed n il
numero di prove, ovvero la numerosità campionaria.
Avremo quindi:
dove X rappresenta il numero di successi ed n il
numero di prove, ovvero la numerosità campionaria.
Avremo quindi:
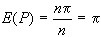


Anche in questo caso,
in base al teorema del limite centrale, la funzione di ripartizione
(FCD) del parametro P potrà essere scritta:

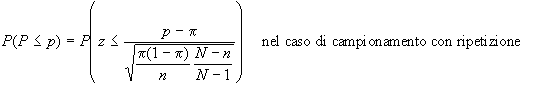
Esempio 1: si è
trovato che il 2% degli utensili prodotti da una macchina
è difettoso. Determinare la probabilità che
in una spedizione di 400 utensile vi sia a) il 3% o più
di difettosi, b) il 4% o meno di difettosi.
a)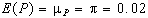 e
e 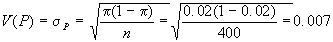 per cui:
per cui:
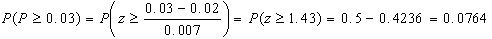
b) 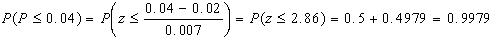
Esempio 2: in un lotto
con N=1000 componenti è presente un 30% di difettosi,
determinare la probabilità di avere in un campione
di n=64 elementi una percentuale di difettosi superiore
al 20%.
E(P)==0.30
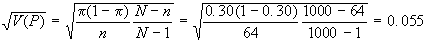
quindi:
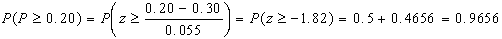
STIMA
DEI PARAMETRI
Molto spesso non è
possibile osservare un'intera popolazione per determinarne
un parametro (ad esempio una medio, il numero di successi,
una proporzione, ecc.), ma si deve ricorrere ad informazioni
parziali per stimare tale parametro. Si ha cioè una
popolazione rispetto alla quale si è interssati ad
un carattere X che avrà una sua distribuzione f(x/),
dove è il valoree incognito di un parametro che identifica
la funzione f(x). Se da questa popolazione si estrae un
campione di n osservazioni si potrà ottenere un valore
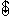 da
utilizzare come stima del parametro della popolazione. Il
problema è quindi di definire una funzione, che applicata
al risultato campionario, offra una stima
da
utilizzare come stima del parametro della popolazione. Il
problema è quindi di definire una funzione, che applicata
al risultato campionario, offra una stima 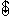 che si possa ritenere una buona stima di . Questa funzione
si dice stimatore e
che si possa ritenere una buona stima di . Questa funzione
si dice stimatore e 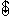 viene detta stima, ed in particolare parleremo di
stima puntuale. E' inoltre possibile, sempre in base ai
risultati campionari, definire un intervallo di stima
entro il quale considerare compreso il valore del parametro
da stimare, con una determinata probabilità di errore.
viene detta stima, ed in particolare parleremo di
stima puntuale. E' inoltre possibile, sempre in base ai
risultati campionari, definire un intervallo di stima
entro il quale considerare compreso il valore del parametro
da stimare, con una determinata probabilità di errore.
1. Stima
per intervalli
La stima puntuale non
fornisce indicazioni riguardo alla probabilità che
lo stimatore utilizzato abbia fornito una stima vicina all'ignoto
valore , per cui spesso si preferisce dare un intervallo
di stima. Si tratta quindi di determinare, in base ai risultati
campionari, gli estremi di un intervallo entro il quale
considerare compreso, con un determinato affidamento, il
valore ignoto del parametro da stimare.
La soluzione a questo
problema è offerta dalla distribuzione campionaria,
infatti noto il modello distributivo di un parametro, oltre
a potere essere utilizzato in senso deduttivo (con quale
probabilità avremo certi valori di tale parametro),
è possibile utilizzarla in senso induttivo (entro
quali intervalli, con una determinata probabilità,
e da ritenersi compreso il valore del parametro della popolazione).
In generale sia X una
v.c. con f(x,) dipendente da ignoto, considerato un campione
di numerosità n che fornisce i valori 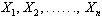 ,
se
,
se 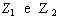 sono due v.c. funzione di
sono due v.c. funzione di 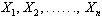 ,
tali che
,
tali che 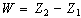 è indipendente da e che:
è indipendente da e che: 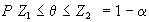 esse determinano un intervallo di confidenza del parametro
avente coefficiente di confidenza pari a 1-.
esse determinano un intervallo di confidenza del parametro
avente coefficiente di confidenza pari a 1-.
Se per tale intervallo
si afferma che al suo interno è compreso l'ignoto
parametro , tale affermazione gode di un grado di fiducia
pari ad 1-.
Per chiarire quanto
detto consideriamo un esempio in cui si ipotizzi una popolazione
in cui sia noto il valore medio del carattere a cui si è
interessati: =69 e =6, e si ipotizzi di costruire campioni
di numerosità n=36.
In base a quanto detto
nel capitolo precedente sappiamo che la distribuzione della
media campionaria sarà: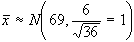 .
Questo ci permetterà di affermare che il 95% della
popolazione è compresa tra 67 e 71. Nella realtà
il parametro è ignoto, e dobbiamo determinarlo in
base ai risultati campionari.
.
Questo ci permetterà di affermare che il 95% della
popolazione è compresa tra 67 e 71. Nella realtà
il parametro è ignoto, e dobbiamo determinarlo in
base ai risultati campionari.
Se supponiamo che un
primo campione estratto casualmente dalla popolazione abbia
fornito una media 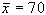 ,
potremo costruire un intervallo:
,
potremo costruire un intervallo: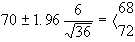
La media campionaria
ottenuta per mezzo del campione osservato è diversa
da quella della popolazione, però quest'ultima ricade
all'interno dell'intervallo che è stato calcolato.
In pratica affermiamo quindi che la media della popolazione
cade all'interno dell'intervallo con una grado di confidenza
del 95%.
Arriviamo a questa affermazione
partendo dalla distribuzione del parametro campionario media,
distribuita, come noto secondo una normale con media pari
a quella della popolazione e s.q.m. pari allo s.q.m. della
popolazione diviso per la radice della numerosità
canpionaria /n. Partendo da questa distribuzione possiamo
costruire un intervallo entro il quale, data come nota la
media della popolazione, ricade ad esempio il 95% delle
medie campionarie calcolate su tutti i possibili campioni
di una certa numerosità. In pratica però non
conosciamo la media della popolazione, che è il parametro
da stimare, possiamo però rovesciare il ragionamento
deduttivo sviluppato fino ad ora, affermando che in un intervallo
costruito su uno dei possibili campioni, quello effettivamente
osservato, di ampiezza sempre 1.96, vi ricadrà la
media della popolazione con una probabilità del 95%.
Questo significa che il 95% di tutti i possibili campioni
che possono essere costruiti danno luogo ad un ntervallo
che contiene la media della popolazione:
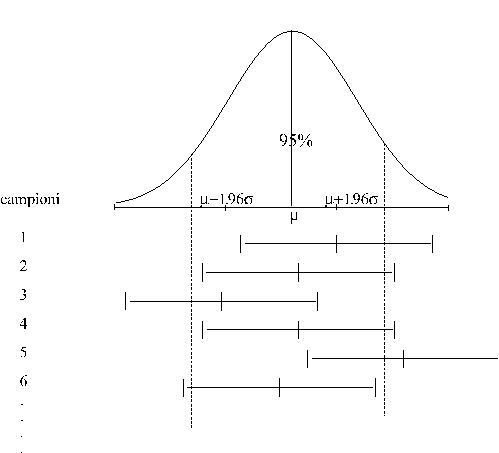
Come si può vedere
dal grafico potremo affermare il 95% dei possibili campioni
fornisce un intervallo (1.96) entro il quale cade la vera
media della popolazione, mentre il 5% dei possibili campioni
presenta un intervallo non contenente la media della popolazione
(ad esempio il campione n.5).
Se volessimo costruire
un intervallo con livello di confidenza superiore, ad esempio
il 99%, gli intervalli saranno più ampi (2.58).
2. Intervalli
di confidenza per la media
Nel caso in cui il parametro
della popolazione da stimare sia la media , dobbiamo considerare
due casi possibili: che sia nota la varianza ² della popolazione,
o che questa sia ignota e debba quindi essere stimata per
mezzo del campione.
2.1 Varianza della popolazione
nota
Dato un campione di
dimensione n estratto da una popolazione con media e varianza
², avremo che, per il teorema del limite centrale:
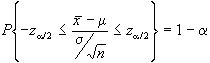
dove -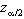 è l'ascissa che lascia /2% dei casi della normale
standardizzata alla sua sinistra, mentre
è l'ascissa che lascia /2% dei casi della normale
standardizzata alla sua sinistra, mentre 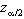 è l'ascissa che lascia a medesima percentuale di
casi alla sua destra.
è l'ascissa che lascia a medesima percentuale di
casi alla sua destra.
Per mezzo di una semplice
trasformazione matematica avremo che la formula precedente
diviene:
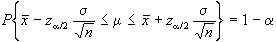
Potremo cioè
dire che la media della popolazione è compresa nell'intervallo:

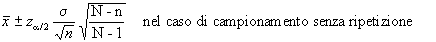
con un grado di affidabilità
dell'1-%.
2.2 Varianza della popolazione
ignota
In questo caso, se la
numerosità del campione è sufficientemente
grande (n30) i limiti dell'intervallo potranno essere calcolati
esattamente con le stesse modalità del caso in cui
la varianza della popolazione sia nota utilizzando come
stima della varianza della popolazione la varianza calcolata
sui dati campionari che indicheremo con s²:
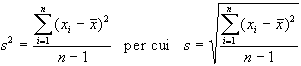
avremo quindi gli intervalli:

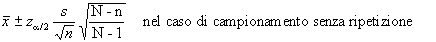
Se invece la numerosità
del campione è inferiore a 30 unità non potremo
più assumere la distribuzione normale come distribuzione
limite; in particolare avremo che:

Gli intervalli saranno
perciò:
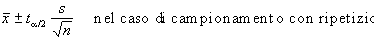

3. Intervalli
di confidenza per una proporzione
Abbiamo già avuto
modo di notare come il parametro proporzione possa essere
considerato come una media 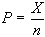 .
.
Pertanto potremo costruire
intervalli di confidenza seguendo una formla del tutto analoga
a quella della media. Quindi se è la proporzione
della popolazione da stimare e p è la proporzione
calcolata sulla base delle osservazioni campionarie, avremo
che:
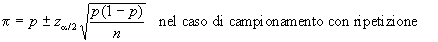
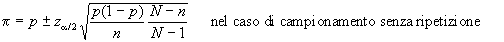
L'approssimazione che
si compie nel sostituire con p per il calcolo della
varianza è ppari a quella che si ha quando si sostituisce
con s, ed introduce una fonte di errore trascurabile per
campioni sufficientemente grandi.
Nel caso di piccoli
campioni sono stati tabultai i valori degli intervalli per
proporzioni da parte di Pearson e Clopper.
Esempio 1: Osservato
un campione con n=50 di rondelle, estratto da una popolazione
con =0.5 mm., si è calcolata una media campionaria
del diametro delle rondelle pari a 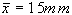 Determinare il diametro medio della produzione da cui è
stato estratto il campione, con un livello di confidenza
del a) 95% e del b) 99%.
Determinare il diametro medio della produzione da cui è
stato estratto il campione, con un livello di confidenza
del a) 95% e del b) 99%.
a) 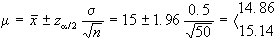
b) 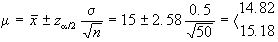
Esempio 2: L'osservazione
di un campione di 200 cuscinetti a sfera ha dato come peso
medio 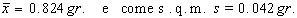 Trovare i limiti di confidenza al 1.a) 95% e 1.b) 99% del
peso medio dei cuscinetti prodotti dalla macchina in esame.
Trovare i limiti di confidenza al 1.a) 95% e 1.b) 99% del
peso medio dei cuscinetti prodotti dalla macchina in esame.
1.a) 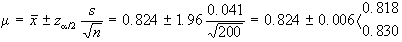
1.b) 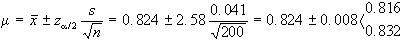
Se il campione osservato
fosse stato di 20 unità, determinare sempre i limiti
di confidenza al 2.a) 95% e 2.b) 99% del peso medio dei
cuscinetti prodotti dalla macchina in esame.
2.a) 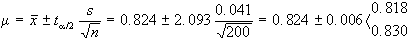
2.b) 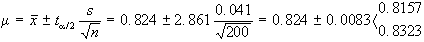
Esempio 3: se in un
campione di 5000 pezzi ne sono stati osservati 60 difettosi,
determinare un intervallo di confidenza al 99% per la proporzione
di difettosi prodotta dalla macchina esaminata.
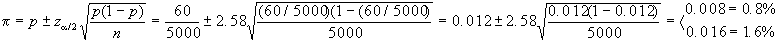
Esempio 4: Nel misurare
il diametro di un bullone, un operatore stima che lo s.q.m.
sia pari a 0.05 cm. Quanto deve essere grande un campione
utilizzato per stimare il diamtero della produzione di bulloni
affinchè possiamo essere "confidenti" a) al 95% e
b) al 99% che l'errore compiuto nella stima non superi il
valore di 0.01 cm.?
a) l'errore di 0.01
cm. corrisponde all'ampiezza dell'intervallo di stima, in
questo caso avremo quindi che: 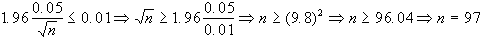
b) 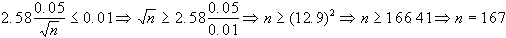
VERIFICA
DELLE IPOTESI
Per ipotesi statistica
intendiamo un'assunzione riguardante generalmente un paramtero
o na distribuzione di una popolazione.
La verifica o controllo
di piotesi consiste nello stabilire se l'assunzione
fatta si possa considerare esatta o meno, sulla base delle
osservazioni campionarie. Un test per provare un'ipotesi
è un criterio per accettare o respingere l'ipotesi
fatta sulla popolazione in base alle risultanze di un campione
estratto da questa popolazione.
L'ipotesi che viene
formulata sul valore che un parametro può asumere,
e che si vuole provare per mezzo del test, è detta
ipotesi nulla H0,
mentre viene indicata con H1
l'ipotesi alternativa, che è l'ipotesi sul
valore che lo stesso parametro può assumere in alternativa
a quello definito nell'ipotesi nulla.
Le ipotesi possono essere:
semplici: se
definiscono un punto nello spazio dei parametri H0:=a
H1:=b
composte: se
definiscono delle regioni H0:=a
H1:a;
H0:a
H1:>a
Nella verifica di ipotesi
si segue la seguente procedura:
definizione
dell'ipotesi nulla
assunzione
della distribuzione del parametro campionario
decisione
del grado di rischio che si è disposti a correre
decisione
sullanumerosità del campione
definizione,
in base ai punti precedenti, della regione critica
o di rifiuto R
estrazione
del campione, calcolo del parametro, controllo con la regione
critica, accettazione o rifiuto dell'ipotesi nulla.
Nel compiere questa
decisione si possono commettere due tipi di errore:
1. rifiutare l'ipotesi
nulla H0
quando in realtà è vera (errore di I tipo)
2. accettare l'ipotesi
nulla H0
quando in realtà è falsa (errore di II
tipo)
La possibilità
di commettere uno di questi errori dipende dal fatto che
la prova di piotesi, essendo di carattere inferenziale,
viene effettuata in condizioni di informazione limitata,
cioè per mezzo di un campione. Questo significa che,
sulla base delle informazioni prodotte da un sottoinsieme
della popolazione, non potremo mai essere sicuri che l'affermazione
fatta nei riguardi della popolazione sia corretta (la certezza
l'avremmo solamente osservando l'intera popolazione).
Ai due tipi di errore
sono associate le probabilità e . In particolare
se 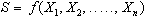 è la funzione test, definiamo:
è la funzione test, definiamo:
1. 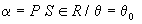 la probabilità di rifiutare H0
quando in realtà è vera (probabilità
errore di I tipo)
la probabilità di rifiutare H0
quando in realtà è vera (probabilità
errore di I tipo)
2. 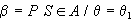 la probabilità che la statistica S cada nella regione
di accettazione A, quando l'ipotesi nulla è falsa.
la probabilità che la statistica S cada nella regione
di accettazione A, quando l'ipotesi nulla è falsa.
Il valore di probabilità
è detto livello di significatività,
e corrisponde alla dimensione della regione critica.
Riassumendo potremo
avere:
| |
ipotesi |
| decisioni |
H0
vera |
H0
falsa |
| respingere
H0
|
errore
I tipo prob= |
decisione
corretta prob=1- |
| accettare
H0
|
decisione
corretta prob=1- |
errore
II tipo prob= |
Esiste una relazione
tra e , tale per cui se diminuiamo la probabilità
di avere un errore di I specie , aumenterà la probabilità
di commettere un errore di seconda specie.
Se consideriamo ad esempio:
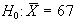
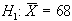
avremo un'area in cui
saremo portati ad accettare 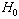 ,
(intervallo A,B). Entro tale intervallo sarà però
possibile commettere un errore di II specie.
,
(intervallo A,B). Entro tale intervallo sarà però
possibile commettere un errore di II specie.
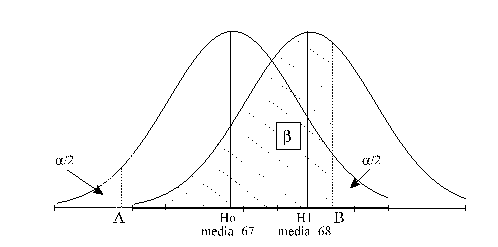
E' chiaro se vogliamo
ridurre la probabilità , dovremo aumentare .
La procedura di verifica
di ipotesi può quindi essere sintetizzata come segue,
nel caso in cui siano prefissati ed n:
definizione
dell'ipotesi nulla 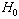
assunzione
della distribuzione del parametro campionario
determinazione
della numerosità campionaria n
definizione
di : livello di significatività
identificazione
della regione critica
estrazione
del campione, calcolo del parametro,
controllo
con la regione critica, e quindi accettazione o rifiuto
dell'ipotesi nulla
controllo
di (detta curva operativa caratteristica OC) o di
1-, detta funzione di potenza, in relazione a prefissate
ipotesi alternative
- se o 1- sono adeguate
alle necessità proprie dell'analisi, confermare la
decisione
- se o 1- sono inadeguate
modificare o n e ripetere il test.
La curva operativa caratteristica
è un grafico indicante la probabilità di errore
di II tipo sotto diverse ipotesi alternative. Questi grafici
forniscono indicazioni riguardo a quanto un test permette
di minimizzare l'errore di II specie; indicano in altri
termini la potenza di un test nell'evitare di prendere decisioni
errate.
Se invece di fissare
a priori i valori di e n, si vuole mantenere controllata
la probabilità di errore di II tipo, potremo sviluppare
un test in cui e sono dati, ed, in base a questi, si determina
la numerosità n del campione da osservare, tale da
soddisfare i livelli di probabilità richiesti. In
questo caso il processo di verifica di ipotesi sarà:
definizione
dell'ipotesi nulla 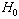
assunzione
della distribuzione del parametro campionario
definizione
di : livello di significatività, e di
calcolo
della numerosità n del campione
identificazione
della regione critica
estrazione
del campione, calcolo del parametro,
controllo
con la regione critica, e quindi accettazione o rifiuto
dell'ipotesi nulla
1. Controllo
di ipotesi sulla media di una popolazione
1.1 Test bilaterale
1. stabilire le ipotesi

2. stabilire il parametro
campionario da utilizzare: 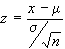
3. decidere il livello
di significatività
4. stabilire la numerosità
campionaria n
5. stabilire i limiti
critici di z in base ad ed n
6. estrarre il campione
e calcolare il valore di z per il campione e controllare
la sua posizione nei confronti dei valori dei limiti
critici
7. decidere se accettare
o rifiutare l'ipotesi nulla
8. individuare, se
necessario, la curva operativa caratteristica
Esempio 1: data la produzione
di una macchina che produce componenti meccanici per i quali
è previsto un diametro di 67mm, con una deviazione
standard di 3mm, decidere, sulla base di un campione di
25 unità se la produzione rispetta le specifiche,
con un livello di significatività del 5%.
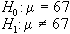
per =5%=0.05 avremo
che i valori limite di z saranno 1.96; graficamente il test
sarà:

Supponiamo di estrarre
il campione e di ottenre 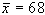 .
.
Calcoliamo 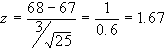
Il valore di z ricade
all'interno dell'intervallo fissato come regione di accettazione:

si è quindi portati
ad accettare l'ipotesi nulla.
Vediamo di determinare
la curva operativa caratteristica. Si ipotizza che alcune
ipotesi alternative siano vere; si considera quindi vera
l'ipotesi =68; sarà la probabilità di avere
campioni con media che ricade nell'intervallo di accettazione
costruito con =67, quando in realtà =68.
I limiti di accettazione
pr =67 saranno:
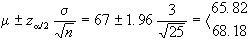
E' sufficiente calcolare
i valori di z per i due limiti:
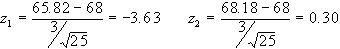
e determinare la probabilità
di avere valori campionari entro questi due limiti, se è
vero che =68:
0.5+0.1172=0.6172.
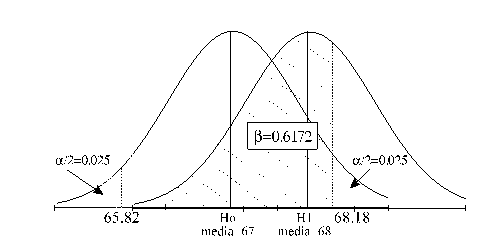
Ripetendo questo calcolo
per diverse alternative avremo:
| |
z1 |
z2 |
|
1- |
| 68.5 |
-4.47 |
-0.53 |
0.29 |
0.71 |
| 68 |
-3.63 |
0.30 |
0.62 |
0.38 |
| 67.5 |
-2.80 |
1.13 |
0.87 |
0.13 |
| 67 |
-1.96 |
1.96 |
0.95 |
0.05 |
| 66.5 |
-1.13 |
2.80 |
0.87 |
0.13 |
| 66 |
-0.30 |
3.63 |
0.62 |
0.38 |
| 65.5 |
0.53 |
4.47 |
0.29 |
0.71 |
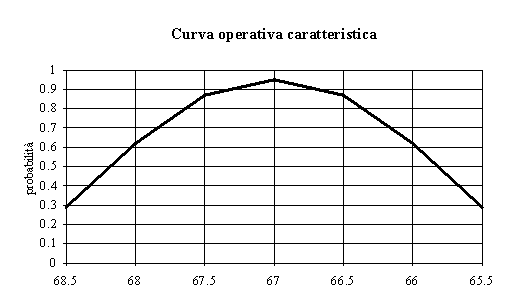
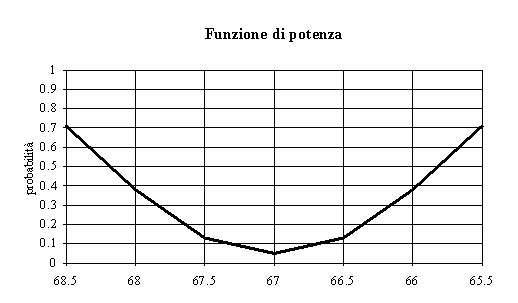
Per diminuire , fissato
, si dovrà modificare la numerosità campionaria
n; quindi pper avere valori di 1- più bassi dovremo
aumentare n. Se consideriamo ad esempio n=100 avremo che
i limiti saranno 66.41 e 67.59, per cui i valori di probabilità
saranno:
|
|
z1 |
z2 |
|
1- |
| 68.5 |
-6.97 |
-3.04 |
0.00 |
1.00 |
| 68 |
-5.30 |
-1.37 |
0.09 |
0.91 |
| 67.5 |
-3.63 |
0.30 |
0.62 |
0.38 |
| 67 |
-1.96 |
1.96 |
0.95 |
0.05 |
| 66.5 |
-0.30 |
3.63 |
0.62 |
0.38 |
| 66 |
1.37 |
5.30 |
0.09 |
0.91 |
| 65.5 |
3.04 |
6.97 |
0.00 |
1.00 |
Graficamente avremo
quindi, confrontando le due curve delle funzioni di potenza:
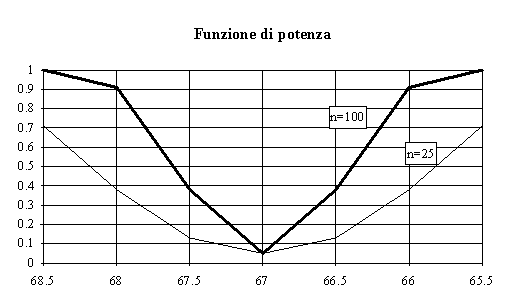
1.2 Test unilaterale
E' il caso in cui si
applica il test per la media ad una sola coda per accettare
l'ipotesi:
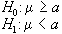 oppure
oppure 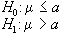
Si applicherà
evidentemente lo stesso procedimento utilizzato nel caso
di test bilaterali, però il limite della regione
di rifiuto sarà determinato in modo che si trovi
da un lato solo della distribuzione del parametro campionario
media.
Esempio: in una miscela
debbono essere presenti 64.3 parti di additivo. Si vuole
verificare con un campione di 25 prove, se la produzione,
con uno scarto quadratico medio =2, assicura la composizione
data, con un livello di significatività =0.05.
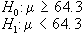
Per =0.05, il limite
di accettazione sarà z=-1.645
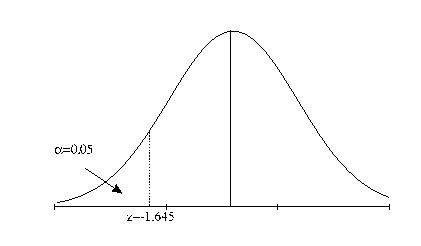
per cui il numero di
parti di additivo che rappresenta il limite della regione
di rifiuto sarà:
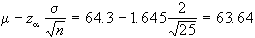
Si rifiuterà
quindi l'ipotesi nulla se il numero medio di parti additivo
nel campione di 25 prove sarà inferiore a 63.64,
oppure se il valore di z calcolato sempre nel campione sarà
inferiore a -1.645.
In questo caso la curva
operativa caratteristica sarà:
| valori
medi alternativi
|
limite
regione rifiuto
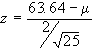
|
curva
operativa caratteristica
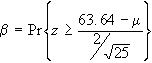 |
| 62.5 |
2.85 |
0.0020 |
| 63 |
1.60 |
0.0548 |
| 63.5 |
0.35 |
0.3632 |
| 64.3 |
-1.645 |
0.9500 |
| 65 |
-3.40 |
0.9997 |
esprime quindi la probabilità di avere valori medi
campionari superiori a 63.4 quando la media della popolazione
è diversa da 63.4:
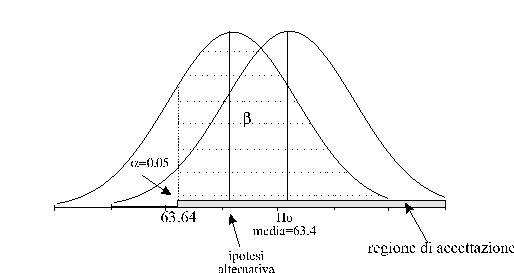
1.3 Determinazione
della numerosità campionaria fissati e
Quando viene fissata
una ipotesi, ed assieme ad essa i valori di probabilità
associati agli errori di I e II specie, si deve determinare
la numerosità minima del campione sufficiente a garantire
i livelli di probabilità desiderati.
Nel caso di test
unilaterali, se indichiamo con K il valore discriminante
che divide la regione di accettazione da quella di rifiuto,
K può essere espresso in termini di si per l'ipotesi
nulla che per quella alternativa, secondo le espressioni:
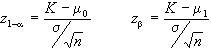
la soluzione del sistema
composto da queste due equazioni consente di determinare
la numerosità campionaria n:
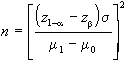
Esempio: sia fissata
l'ipotesi: 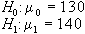 con =16 ed inoltre siano dati =0.05 e =0.20, determinare
la numerosità n del campione.
con =16 ed inoltre siano dati =0.05 e =0.20, determinare
la numerosità n del campione.
Avremo quindi: 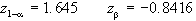 per
cui
per
cui
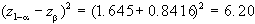
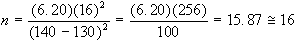
Nel caso di test
bilaterali avremo che la numerosità del campione
sarà data da:
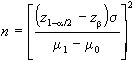
1.4 Test di
ipotesi per la media nel caso di ignota
In questo caso si dovrà
utilizzare la distribuzione del parametro campionario t-Student:
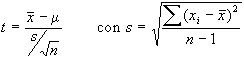
con n-1 gradi di libertà,
purchè la popolazione di provenienza possa essere
considerata normale.
Esempio test bilaterale:
data una macchina che
effettua le pesatura automatica per il riempimento di sacchetti
contenenti 65 gr. di prodotto: si vuole controllare se la
macchina mantiene il suo standard. Vengono registrate 12
pesate: 55, 62,54,58,65,64,60,62,59,67,62,61; e si vuole
operare il controllo al livello del 5%.
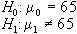
Avremo quindi una distribuzione
t con (n-1)=(12-1)=11 gradi di libertà da cui otterremo:

in base al campione
avremo inoltre:  potremo quindi calcolare il valore di t nel campione:
potremo quindi calcolare il valore di t nel campione:
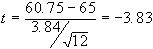
per cui rifiuteremo
l'ipotesi nulla.
Esempio test unilaterale:
data una miscela chimica
in cui debbono essere presenti almeno 64.3 parti di un additivo,
si vuole verificare con 25 prove se la produzione garatisce
tale tipo di composizione della miscela al livello del 5%.
Il campione di 25 prove ha presentato: 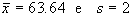 .
.
In questo caso i gradi
di libertà saranno (25-1)=24, per cui la soglia del
valore t sarà: t-1.711.
Il valore del t campionario
è invece:
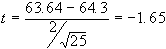
per cui potremo accettare
l'ipotesi nulla.
2. Controllo
di ipotesi sulla proporzione di una popolazione
In questo caso il paramtero
campionario sarà 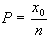 ,
dove
,
dove 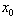 rappresenta il numero di elementi del campione che hanno
la caratteristica da controllare.
rappresenta il numero di elementi del campione che hanno
la caratteristica da controllare.
Come noto la proporzione
ha una distribuzione binomiale, che però si approssima
alla normale per valori di n sufficientemente grandi e P
no troppo piccolo. Il parametro P potrà quindi essere
assimilato alla media campionaria. Perciò se np5
si potrà fare riferimento alla distribuzione z:
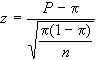
In base a questa si
potranno quindi determinare i valori critici in base ad
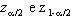 in
caso di test unilaterale o bilaterale.
in
caso di test unilaterale o bilaterale.
Esempio: dato un campione
di 50 unità di prodotto, nel quale è stato
osservato un 5% di pezzi difettosi, si verifichi l'ipotesi
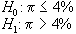 che
la produzione complessiva presenta meno del 4% di difettosi,
con un livello di significatività del 5%.
che
la produzione complessiva presenta meno del 4% di difettosi,
con un livello di significatività del 5%.
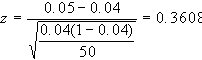
Siccome la soglia critica
del test unilaterale per =0.05 è z=1.64, accetteremo
l'ipotesi nulla.